


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-2-2020
Date: 4-2-2020
Date: 14-1-2020
|
In Moralia, the Greek biographer and philosopher Plutarch states "Chrysippus says that the number of compound propositions that can be made from only ten simple propositions exceeds a million. (Hipparchus, to be sure, refuted this by showing that on the affirmative side there are 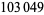 compound statements, and on the negative side
compound statements, and on the negative side 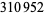 .)" These numbers are known as the Plutarch numbers.
.)" These numbers are known as the Plutarch numbers.
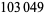 can be interpreted as the number
can be interpreted as the number 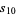 of bracketings on ten letters (Stanley 1997, Habsieger et al. 1998). Similarly, Plutarch's second number is given by
of bracketings on ten letters (Stanley 1997, Habsieger et al. 1998). Similarly, Plutarch's second number is given by 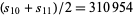 (Habsieger et al. 1998).
(Habsieger et al. 1998).
REFERENCES:
Biermann, K.-R. and Mau, J. "Überprüfung einer frühen Anwendung der Kombinatorik in der Logik." J. Symbolic Logic 23, 129-132, 1958.
Biggs, N. L. "The Roots of Combinatorics." Historia Mathematica 6, 109-136, 1979.
Habsieger, L.; Kazarian, M.; and Lando, S. "On the Second Number of Plutarch." Amer. Math. Monthly 105, 446, 1998.
Heath, T. L. A History of Greek Mathematics, Vol. 2: From Aristarchus to Diophantus. New York: Dover, p. 256, 1981.
Kneale, W. and Kneale, M. The Development of Logic. Oxford, England: Oxford University Press, p. 162, 1971.
Neugebauer, O. A History of Ancient Mathematical Astronomy. New York: Springer-Verlag, p. 338, 1975.
Plutarch. §VIII.9 in Moralia, Vol. 9. Cambridge, MA: Harvard University Press, p. 732, 1961.
Stanley, R. P. Enumerative Combinatorics, Vol. 1. Cambridge, England: Cambridge University Press, p. 63, 1996.
Stanley, R. P. "Hipparchus, Plutarch, Schröder, and Hough." Amer. Math. Monthly 104, 344-350, 1997.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|