Stieltjes Constants

Expanding the Riemann zeta function about 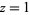 gives

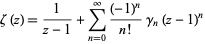(1)

(Havil 2003, p. 118), where the constants

(2)

are known as Stieltjes constants.

Another sum that can be used to define the constants is

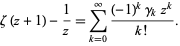(3)

These constants are returned by the Wolfram Language function StieltjesGamma[n].

A generalization 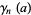 takes 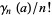 as the coefficient of  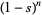is the Laurent series of the Hurwitz zeta function  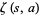about 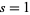. These generalized Stieltjes constants are implemented in the Wolfram Language as StieltjesGamma[n, a].

The case 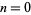 gives the usual Euler-Mascheroni constant

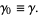(4)

A limit formula for 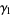 is given by

(5)

where  is the imaginary part and 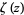 is the Riemann zeta function.

An alternative definition is given by absorbing the coefficient of 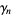 into the constant,

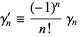(6)

(e.g., Hardy 1912, Kluyver 1927).

The Stieltjes constants are also given by

(7)

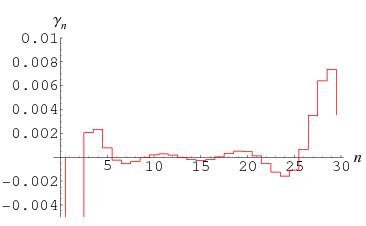
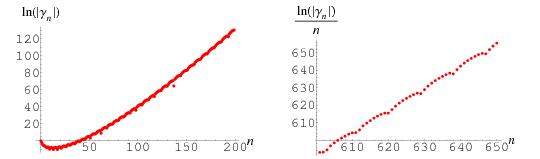
Plots of the values of the Stieltjes constants as a function of 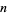 are illustrated above (Kreminski). The first few numerical values are given in the following table.

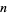	OEIS
0	A001620	0.5772156649
1	A082633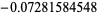
2	A086279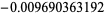
3	A086280	0.002053834420
4	A086281	0.002325370065
5	A086282	0.0007933238173

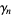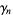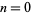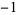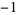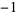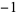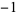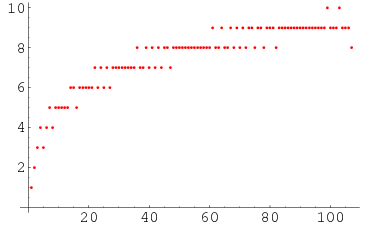
Briggs (1955-1956) proved that there infinitely many  of each sign. The signs of  for , 1, ... are 1, , , 1, 1, 1, , , , , 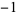... (OEIS A114523), and the run lengths of consecutive signs are 1, 2, 3, 4, 3, 4, 5, 4, 5, 5, 5, ... (OEIS A114524). A plot of run lengths is shown above.

Berndt (1972) gave upper bounds of

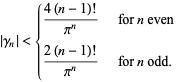(8)

However, these bounds are extremely weak. A stronger bound is given by

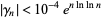(9)

for 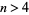 (Matsuoka 1985).

Vacca (1910) proved that the Euler-Mascheroni constant may be expressed as

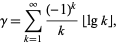(10)

where 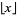 is the floor function and the lg function  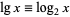is the logarithm to base 2. Hardy (1912) derived the formula

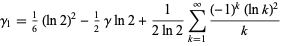(11)

from Vacca's expression.

Kluyver (1927) gave similar series for 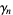 valid for all ,

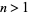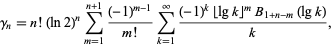(12)

where 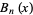 is a Bernoulli polynomial. However, this series converges extremely slowly, requiring more than  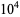terms to get two digits of  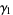and many more for higher order .

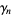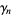 can also be expressed as a single sum using

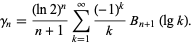(13)

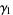 also appears in the asymptotic expansion of the sum

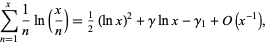(14)

where 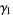 was called  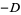and given incorrectly by Ellision and Mendès-France (1975) (and the error was subsequently reproduced by Le Lionnais 1983, p. 47). The exact form of (14) is given by

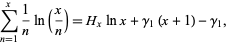(15)

where 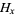 is a harmonic number and  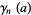is a generalized Stieltjes constant.

A set of constants related to 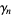 is

(16)

(Sitaramachandrarao 1986, Lehmer 1988).

The Stieltjes constants also satisfy the beautiful sum

(17)

(O. Marichev, pers. comm., 2008).

REFERENCES:

Berndt, B. C. "On the Hurwitz Zeta-Function." Rocky Mountain J. Math. 2, 151-157, 1972.

Bohman, J. and Fröberg, C.-E. "The Stieltjes Function--Definitions and Properties." Math. Comput. 51, 281-289, 1988.

Briggs, W. E. "Some Constants Associated with the Riemann Zeta-Function." Mich. Math. J. 3, 117-121, 1955-1956.

Coffey, M. W. "New Results on the Stieltjes Constants: Asymptotic and Exact Evaluation." J. Math. Anal. Appl. 317, 603-612, 2006.

Coffey, M. W. "New Summation Relations for the Stieltjes Constants." Proc. Roy. Soc. A 462, 2563-2573, 2006.

Ellison, W. J. and Mendès-France, M. Les nombres premiers. Paris: Hermann, 1975.

Finch, S. R. "Stieltjes Constants." §2.21 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 166-171, 2003.

Hardy, G. H. "Note on Dr. Vacca's Series for 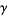." Quart. J. Pure Appl. Math. 43, 215-216, 1912.

Hardy, G. H. and Wright, E. M. "The Behavior of 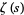 when 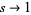." §17.3 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 246-247, 1979.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Kluyver, J. C. "On Certain Series of Mr. Hardy." Quart. J. Pure Appl. Math. 50, 185-192, 1927.

Knopfmacher, J. "Generalised Euler Constants." Proc. Edinburgh Math. Soc. 21, 25-32, 1978.

Kreminski, R. "Newton-Cotes Integration for Approximating Stieltjes (Generalized Euler) Constants." Math. Comput. 72, 1379-1397, 2003.

Kreminski, R. "This Site Will Archive Some Stieltjes-Related Computational Work..." http://www.tamu-commerce.edu/math/FACULTY/KREMIN/stieltjesrelated/.

Kreminski, R. "This Page Displays Work in Progress by Rick Kreminski." http://www.tamu-commerce.edu/math/FACULTY/KREMIN/stieltjes/stieltjestestpage.html.

Kreminski, R. "Gammas 1 to 12 to 6900 Digits." http://www.tamu-commerce.edu/math/FACULTY/KREMIN/stieltjesrelated/gammas1to12/.

Lammel, E. "Ein Beweis dass die Riemannsche Zetafunktion 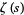 is 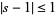 keine Nullstelle besitzt." Univ. Nac. Tucmán Rev. Ser. A 16, 209-217, 1966.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 47, 1983.

Lehmer, D. H. "The Sum of Like Powers of the Zeros of the Riemann Zeta Function." Math. Comput. 50, 265-273, 1988.

Liang, J. J. Y. and Todd, J. "The Stieltjes Constants." J. Res. Nat. Bur. Standards--Math. Sci. 76B, 161-178, 1972.

Matsuoka, Y. "Generalized Euler Constants Associated with the Riemann Zeta Function." In Number Theory and Combinatorics. Japan 1984 (Tokyo, Okayama and Kyoto, 1984). Singapore: World Scientific, pp. 279-295, 1985.

Plouffe, S. "Stieltjes Constants from 0 to 78, to 256 Digits Each." http://pi.lacim.uqam.ca/piDATA/stieltjesgamma.txt.

Sitaramachandrarao, R. "Maclaurin Coefficients of the Riemann Zeta Function." Abstracts Amer. Math. Soc. 7, 280, 1986.

Sloane, N. J. A. Sequences A001620/M3755, A082633, A086279, A086280, A086281, A086282, A114523, and A114524 in "The On-Line Encyclopedia of Integer Sequences."

Vacca, G. "A New Series for the Eulerian Constant." Quart. J. Pure Appl. Math. 41, 363-368, 1910.