


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-11-2020
Date: 12-11-2019
Date: 24-8-2020
|

The triangular number  is a figurate number that can be represented in the form of a triangular grid of points where the first row contains a single element and each subsequent row contains one more element than the previous one. This is illustrated above for
is a figurate number that can be represented in the form of a triangular grid of points where the first row contains a single element and each subsequent row contains one more element than the previous one. This is illustrated above for  ,
,  , .... The triangular numbers are therefore 1,
, .... The triangular numbers are therefore 1,  ,
,  ,
,  , ..., so for
, ..., so for  , 2, ..., the first few are 1, 3, 6, 10, 15, 21, ... (OEIS A000217).
, 2, ..., the first few are 1, 3, 6, 10, 15, 21, ... (OEIS A000217).
More formally, a triangular number is a number obtained by adding all positive integers less than or equal to a given positive integer 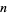 , i.e.,
, i.e.,
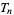 |
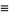 |
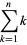 |
(1) |
 |
 |
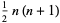 |
(2) |
 |
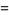 |
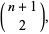 |
(3) |
where 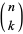 is a binomial coefficient. As a result, the number of distinct wine glass clinks that can be made among a group of
is a binomial coefficient. As a result, the number of distinct wine glass clinks that can be made among a group of 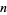 people (which is simply
people (which is simply 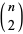 ) is given by the triangular number
) is given by the triangular number 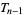 .
.
The triangular number 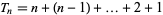 is therefore the additive analog of the factorial
is therefore the additive analog of the factorial 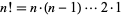 .
.

A plot of the first few triangular numbers represented as a sequence of binary bits is shown above. The top portion shows 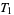 to
to 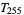 , and the bottom shows the next 510 values.
, and the bottom shows the next 510 values.
The odd triangular numbers are given by 1, 3, 15, 21, 45, 55, ... (OEIS A014493), while the even triangular numbers are 6, 10, 28, 36, 66, 78, ... (OEIS A014494).
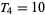 gives the number and arrangement of the tetractys (which is also the arrangement of bowling pins), while
gives the number and arrangement of the tetractys (which is also the arrangement of bowling pins), while 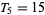 gives the number and arrangement of balls in billiards. Triangular numbers satisfy the recurrence relation
gives the number and arrangement of balls in billiards. Triangular numbers satisfy the recurrence relation
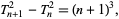 |
(4) |
as well as
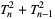 |
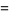 |
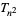 |
(5) |
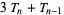 |
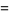 |
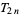 |
(6) |
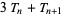 |
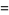 |
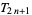 |
(7) |
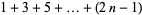 |
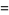 |
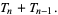 |
(8) |

In addition, the triangle numbers can be related to the square numbers by
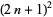 |
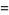 |
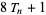 |
(9) |
 |
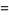 |
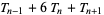 |
(10) |
(Conway and Guy 1996), as illustrated above (Wells 1991, p. 198).
The triangular numbers have the ordinary generating function
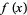 |
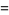 |
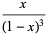 |
(11) |
 |
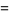 |
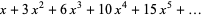 |
(12) |
and exponential generating function
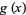 |
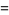 |
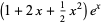 |
(13) |
 |
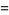 |
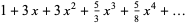 |
(14) |
 |
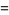 |
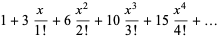 |
(15) |
(Sloane and Plouffe 1995, p. 9).
Every other triangular number 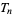 is a hexagonal number, with
is a hexagonal number, with
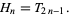 |
(16) |
In addition, every pentagonal number is 1/3 of a triangular number, with
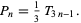 |
(17) |
The sum of consecutive triangular numbers is a square number, since
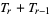 |
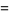 |
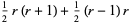 |
(18) |
 |
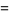 |
![1/2r[(r+1)+(r-1)]](https://mathworld.wolfram.com/images/equations/TriangularNumber/Inline67.gif) |
(19) |
 |
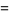 |
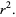 |
(20) |
Interesting identities involving triangular, square, and cubic numbers are
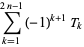 |
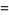 |
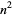 |
(21) |
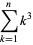 |
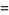 |
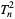 |
(22) |
 |
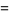 |
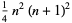 |
(23) |
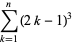 |
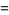 |
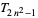 |
(24) |
 |
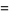 |
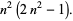 |
(25) |
Triangular numbers also unexpectedly appear in integrals involving the absolute value of the form
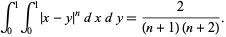 |
(26) |
All even perfect numbers are triangular 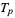 with prime
with prime 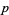 . Furthermore, every even perfect number
. Furthermore, every even perfect number 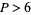 is of the form
is of the form
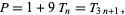 |
(27) |
where 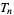 is a triangular number with
is a triangular number with 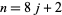 (Eaton 1995, 1996). Therefore, the nested expression
(Eaton 1995, 1996). Therefore, the nested expression
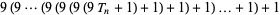 |
(28) |
generates triangular numbers for any 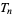 . An integer
. An integer 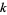 is a triangular number iff
is a triangular number iff 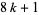 is a square number
is a square number 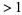 .
.
The numbers 1, 36, 1225, 41616, 1413721, 48024900, ... (OEIS A001110) are square triangular numbers, i.e., numbers which are simultaneously triangular and square (Pietenpol 1962). The corresponding square roots are 1, 6, 35, 204, 1189, 6930, ... (OEIS A001109), and the indices of the corresponding triangular numbers 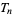 are
are 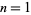 , 8, 49, 288, 1681, ... (OEIS A001108).
, 8, 49, 288, 1681, ... (OEIS A001108).
Numbers which are simultaneously triangular and tetrahedral satisfy the binomial coefficient equation
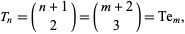 |
(29) |
the only solutions of which are
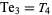 |
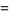 |
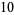 |
(30) |
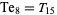 |
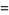 |
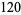 |
(31) |
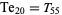 |
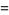 |
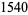 |
(32) |
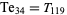 |
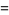 |
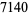 |
(33) |
(Guy 1994, p. 147).
The following table gives triangular numbers 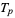 having prime indices
having prime indices 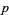 .
.
| class | Sloane | sequence |
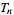 with prime indices with prime indices |
A034953 | 3, 6, 15, 28, 66, 91, 153, 190, 276, 435, 496, ... |
odd 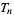 with prime indices with prime indices |
A034954 | 3, 15, 91, 153, 435, 703, 861, 1431, 1891, 2701, ... |
even 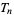 with prime indices with prime indices |
A034955 | 6, 28, 66, 190, 276, 496, 946, 1128, 1770, 2278, ... |
The smallest of two integers for which 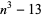 is four times a triangular number is 5, as determined by Cesàro in 1886 (Le Lionnais 1983, p. 56). The only Fibonacci numbers which are triangular are 1, 3, 21, and 55 (Ming 1989), and the only Pell number which is triangular is 1 (McDaniel 1996). The beast number 666 is triangular, since
is four times a triangular number is 5, as determined by Cesàro in 1886 (Le Lionnais 1983, p. 56). The only Fibonacci numbers which are triangular are 1, 3, 21, and 55 (Ming 1989), and the only Pell number which is triangular is 1 (McDaniel 1996). The beast number 666 is triangular, since
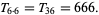 |
(34) |
In fact, it is the largest repdigit triangular number (Bellew and Weger 1975-76).
The positive divisors of 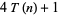 are all of the form
are all of the form 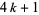 , those of
, those of 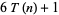 are all of the form
are all of the form 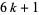 , and those of
, and those of 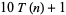 are all of the form
are all of the form 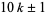 ; that is, they end in the decimal digit 1 or 9.
; that is, they end in the decimal digit 1 or 9.
Fermat's polygonal number theorem states that every positive integer is a sum of at most three triangular numbers, four square numbers, five pentagonal numbers, and 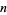
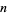 -polygonal numbers. Gauss proved the triangular case (Wells 1986, p. 47), and noted the event in his diary on July 10, 1796, with the notation
-polygonal numbers. Gauss proved the triangular case (Wells 1986, p. 47), and noted the event in his diary on July 10, 1796, with the notation
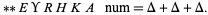 |
(35) |
This case is equivalent to the statement that every number of the form 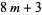 is a sum of three odd squares (Duke 1997). Dirichlet derived the number of ways in which an integer
is a sum of three odd squares (Duke 1997). Dirichlet derived the number of ways in which an integer 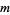 can be expressed as the sum of three triangular numbers (Duke 1997). The result is particularly simple for a prime of the form
can be expressed as the sum of three triangular numbers (Duke 1997). The result is particularly simple for a prime of the form 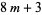 , in which case it is the number of squares mod
, in which case it is the number of squares mod 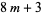 minus the number of nonsquares mod
minus the number of nonsquares mod 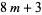 in the interval from 1 to
in the interval from 1 to 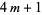 (Deligne 1973, Duke 1997).
(Deligne 1973, Duke 1997).
The only triangular numbers which are the product of three consecutive integers are 6, 120, 210, 990, 185136, 258474216 (OEIS A001219; Guy 1994, p. 148).
REFERENCES:
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 59, 1987.
Bellew, D. W. and Weger, R. C. "Repdigit Triangular Numbers." J. Recr. Math. 8, 96-97, 1975-76.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 33-38, 1996.
Deligne, P. "La Conjecture de Weil." Inst. Hautes Études Sci. Pub. Math. 43, 273-308, 1973.
Dudeney, H. E. Amusements in Mathematics. New York: Dover, pp. 67 and 167, 1970.
Duke, W. "Some Old Problems and New Results about Quadratic Forms." Not. Amer. Math. Soc. 44, 190-196, 1997.
Eaton, C. F. "Problem 1482." Math. Mag. 68, 307, 1995.
Eaton, C. F. "Perfect Number in Terms of Triangular Numbers." Solution to Problem 1482. Math. Mag. 69, 308-309, 1996.
Guy, R. K. "Sums of Squares" and "Figurate Numbers." §C20 and §D3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 136-138 and 147-150, 1994.
Hindin, H. "Stars, Hexes, Triangular Numbers and Pythagorean Triples." J. Recr. Math. 16, 191-193, 1983-1984.
Hobson, N. "Triangular Numbers." https://www.qbyte.org/puzzles/p149s.html#triangular.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 56, 1983.
McDaniel, W. L. "Triangular Numbers in the Pell Sequence." Fib. Quart. 34, 105-107, 1996.
Ming, L. "On Triangular Fibonacci Numbers." Fib. Quart. 27, 98-108, 1989.
Pappas, T. "Triangular, Square & Pentagonal Numbers." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 214, 1989.
Pietenpol, J. L. "Square Triangular Numbers." Amer. Math. Monthly 169, 168-169, 1962.
Ram, R. "Triangle Numbers that are Perfect Squares." https://users.tellurian.net/hsejar/maths/triangle/.
Satyanarayana, U. V. "On the Representation of Numbers as the Sum of Triangular Numbers." Math. Gaz. 45, 40-43, 1961.
Sloane, N. J. A. Sequences A000217/M2535, A001108/M4536, A001109/M4217, A001110/M5259, A001219, A014493, A014494, A034953, A034955, and A034955 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego, CA: Academic Press, 1995.
Trotter, T. Jr. "Some Identities for the Triangular Numbers." J. Recr. Math. 6, 128-135, 1973.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 47-48, 1986.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 199, 1991.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|