


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-9-2020
Date: 4-5-2020
Date: 2-11-2019
|
Given the sum-of-factorials function
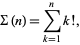 |
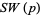 is the smallest integer for
is the smallest integer for 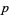 prime such that
prime such that ![Sigma[SW(p)]](https://mathworld.wolfram.com/images/equations/Smarandache-WagstaffFunction/Inline3.gif) is divisible by
is divisible by 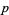 . If
. If 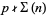 for all
for all 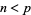 , then
, then 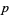 never divides any sum for all
never divides any sum for all 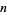 . Therefore, the values
. Therefore, the values 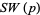 do not exist for 2, 5, 7, 13, 19, 31, ... (OEIS A056985).
do not exist for 2, 5, 7, 13, 19, 31, ... (OEIS A056985).
The function is defined for 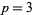 , 11, 17, 23, 29, 37, 41, 43, 53, 67, 73, 79, 97, ... (OEIS A056983), with corresponding values 2, 4, 5, 12, 19, 24, 32, 19, 20, 20, 20, 7, 57, 6, ... (OEIS A056985).
, 11, 17, 23, 29, 37, 41, 43, 53, 67, 73, 79, 97, ... (OEIS A056983), with corresponding values 2, 4, 5, 12, 19, 24, 32, 19, 20, 20, 20, 7, 57, 6, ... (OEIS A056985).
REFERENCES:
Ashbacher, C. "Some Properties of the Smarandache-Kurepa and Smarandache-Wagstaff Functions." Math. Informatics Quart. 7, 114-116, 1997.
"Functions in Number Theory." https://www.gallup.unm.edu/~smarandache/FUNCT1.TXT.
Mudge, M. "Introducing the Smarandache-Kurepa and Smarandache-Wagstaff Functions." Smarandache Notions J. 7, 52-53, 1996.
Mudge, M. "Introducing the Smarandache-Kurepa and Smarandache-Wagstaff Functions." Abstracts of Papers Presented to the Amer. Math. Soc. 17, 583, 1996.
Sloane, N. J. A. Sequences A056983, A056984, and A056985 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|