


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-8-2020
Date: 5-8-2020
Date: 20-12-2020
|
Pick two real numbers  and
and 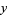 at random in
at random in 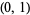 with a uniform distribution. What is the probability
with a uniform distribution. What is the probability 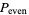 that
that ![[x/y]](https://mathworld.wolfram.com/images/equations/RealNumberPicking/Inline5.gif) , where
, where ![[r]](https://mathworld.wolfram.com/images/equations/RealNumberPicking/Inline6.gif) denotes the nearest integer function, is even?
denotes the nearest integer function, is even?
The answer may be found as follows.
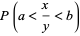 |
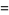 |
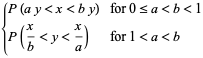 |
(1) |
 |
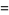 |
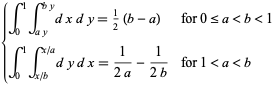 |
(2) |
so
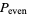 |
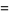 |
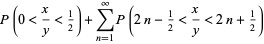 |
(3) |
 |
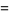 |
![1/2(1/2-0)+sum_(n=1)^(infty)[1/(2(2n-1/2))-1/(2(2n+1/2))]](https://mathworld.wolfram.com/images/equations/RealNumberPicking/Inline18.gif) |
(4) |
 |
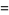 |
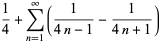 |
(5) |
 |
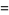 |
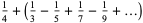 |
(6) |
 |
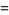 |
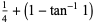 |
(7) |
 |
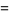 |
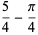 |
(8) |
 |
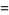 |
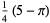 |
(9) |
 |
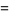 |
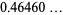 |
(10) |
(OEIS A091651).
REFERENCES:
American Mathematics Competitions. Problem B3 in "William Lowell Putnam Competition Archive, 1993" https://www.unl.edu/amc/a-activities/a7-problems/putnam/.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, p. 139, 2003.
Losinski, L. F.; Alexanderson, G. L.; and Larson, L. C. "The Fifty-Fourth William Lowell Putnam Mathematical Competition." Amer. Math. Monthly 101, 725-734, 1994.
Scholes, J. "54th Putnam 1993." https://www.kalva.demon.co.uk/putnam/putn93.html.
Sloane, N. J. A. Sequence A091651 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|