


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-12-2020
Date: 8-7-2020
Date: 4-7-2020
|
The von Staudt-Clausen theorem, sometimes also known as the Staudt-Clausen theorem (Carlitz 1968), states that
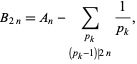 |
(1) |
where 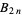 is a Bernoulli number,
is a Bernoulli number, 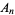 is an integer, and the
is an integer, and the 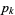 s are the primes satisfying
s are the primes satisfying 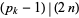 , i.e.,
, i.e., 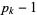 divides
divides 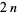 .
.
For example, for 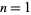 , the primes included in the sum are 2 and 3, since
, the primes included in the sum are 2 and 3, since 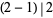 and
and 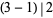 , giving
, giving
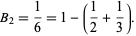 |
(2) |
Similarly, for 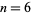 , the included primes are (2, 3, 5, 7, 13), since (1, 2, 4, 6, 12) divide
, the included primes are (2, 3, 5, 7, 13), since (1, 2, 4, 6, 12) divide 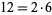 , giving
, giving
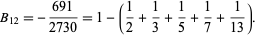 |
(3) |
The first few values of 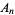 for
for 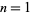 , 2, ... are 1, 1, 1, 1, 1, 1, 2,
, 2, ... are 1, 1, 1, 1, 1, 1, 2, 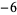 , 56,
, 56, 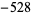 , ... (OEIS A000146), and the lists of primes appearing in successive sums are 2, 3; 2, 3, 5; 2, 3, 7; 2, 3, 5; 2, 3, 11; ... (OEIS A080092).
, ... (OEIS A000146), and the lists of primes appearing in successive sums are 2, 3; 2, 3, 5; 2, 3, 7; 2, 3, 5; 2, 3, 11; ... (OEIS A080092).
The theorem was rediscovered by Ramanujan (Hardy 1999, p. 11) and can be proved using p-adic Numbers.
REFERENCES:
Carlitz, L. "Bernoulli Numbers." Fib. Quart. 6, 71-85, 1968.
Clausen, T. "Theorem." Astron. Nach. 17, 351-352, 1840.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 109, 1996.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Wright, E. M. "The Theorem of von Staudt" and "Proof of von Staudt's Theorem." §7.9-7.10 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 90-93, 1979.
Rado, R. "A New Proof of a Theorem of V. Staudt." J. London Math. Soc. 9, 85-88, 1934.
Rado, R. "A Note on the Bernoullian Numbers." J. London Math. Soc. 9, 88-90, 1934.
Sloane, N. J. A. Sequences A000146/M1717 and A080092 in "The On-Line Encyclopedia of Integer Sequences."
Staudt, K. G. C. von. "Beweis eines Lehrsatzes, die Bernoullischen Zahlen betreffend." J. reine angew. Math. 21, 372-374, 1840.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|