Wagstaff Prime

A Wagstaff prime is a prime number of the form 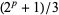 for 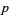 a prime number. The first few are given by 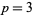, 5, 7, 11, 13, 17, 19, 23, 31, 43, 61, 79, 101, 127, 167, 191, 199, 313, 347, 701, 1709, 2617, 3539, 5807, 10501, 10691, 11279, 12391, 14479, 42737, 83339, 95369, 117239, 127031, 138937, 141079, 267017, 269987, 374321, 986191, and 4031399 (OEIS A000978), with  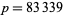and larger corresponding to probable primes. These values  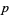correspond to the primes  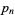with indices 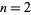, 3, 4, 5, 6, 7, 8, 9, 11, 14, 18, 22, 26, ... (OEIS A123176).

The Wagstaff primes are featured in the new Mersenne prime conjecture.

There is no simple primality test analogous to the Lucas-Lehmer test for Wagstaff primes, so all recent primality proofs of Wagstaff primes have used elliptic curve primality proving.

A Wagstaff prime can also be interpreted as a repunit prime of base 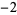, as

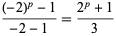if  is odd, as it must be for the above number to be prime.

Some of the largest known Wagstaff probable primes are summarized in the following table, with the largest two being the largest two known probable primes as of Sep. 2013 (Propper 2013; Lifchitz and Lifchitz) but not necessarily the sequentially next primes after .

	decimal digits	discoverer
374321		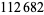H. R. Lifchitz (Dec. 2000)
986191		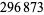V. Diepeveen (Jun. 2008)
4031399		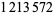T. Reix et al. (Feb. 2010)
13347311		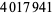R. Propper (Sep. 2013)
13372531		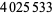R. Propper (Sep. 2013)

REFERENCES:

Bateman, P. T.; Selfridge, J. L.; and Wagstaff, S. S. "The New Mersenne Conjecture." Amer. Math. Monthly 96, 125-128, 1989.

Caldwell, C. "New Mersenne Prime Conjecture." https://primes.utm.edu/glossary/page.php?sort=NewMersenneConjecture.

Caldwell, C. "Wagstaff Prime." https://primes.utm.edu/top20/page.php?id=67.

Lifchitz, H. and Lifchitz, R. "PRP Records: Probable Primes Top 10000."

Morain, F. "Distributed Primality Proving and the Primality of 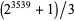." In Advances in cryptology--EUROCRYPT '90. Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques held in Aarhus, May 21-24, 1990 (Ed. I. B. Damgård). Berlin: Springer, pp. 110-123, 1991.

Propper, R. "New Wagstaff PRP Exponents." 08 Sep 2013. https://www.mersenneforum.org/showpost.php?p=352430.

Sloane, N. J. A. Sequences A000978/M2413 and A123176 in "The On-Line Encyclopedia of Integer Sequences."