


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-10-2020
Date: 9-8-2020
Date: 8-11-2020
|
Let the difference of successive primes be defined by 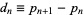 , and
, and 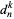 by
by
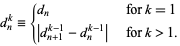 |
(1) |
N. L. Gilbreath claimed that 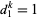 for all
for all 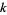 (Guy 1994). In 1959, the claim was verified for
(Guy 1994). In 1959, the claim was verified for 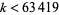 . In 1993, Odlyzko extended the claim to all primes up to
. In 1993, Odlyzko extended the claim to all primes up to 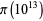 .
.
Gilbreath's conjecture is equivalent to the statement that, in the triangular array of the primes, iteratively taking the absolute difference of each pair of terms
 |
(2) |
(OEIS A036262), always gives leading term 1 (after the first row).
The number of terms before reaching the first greater than two in the second, third, etc., rows are given by 3, 8, 14, 14, 25, 23, 22, 25, ... (OEIS A000232).
REFERENCES:
Caldwell, C. K. "Gilbreath's Conjecture." https://primes.utm.edu/glossary/page.php?sort=GilbreathsConjecture.
Debono, A. N. "Numbers and Computers (11): More on Primes." https://www.eng.um.edu.mt/~andebo/numbers/numcom11.htm.
Gardner, M. "Patterns in Primes are a Clue to the Strong Law of Small Numbers." Sci. Amer. 243, 18-28, Dec. 1980.
Guy, R. K. "Gilbreath's Conjecture." §A10 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 25-26, 1994.
Kilgrove, R. B. and Ralston, K. E. "On a Conjecture Concerning the Primes." Math. Tables Aids Comput. 13, 121-122, 1959.
Odlyzko, A. M. "Iterated Absolute Values of Differences of Consecutive Primes." Math. Comput. 61, 373-380, 1993.
Proth, F. "Sur la série des nombres premiers." Nouv. Corresp. Math 4, 236-240, 1878.
Sloane, N. J. A. Sequences A000232/M2718 and A036262 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|