abc Conjecture

The abc conjecture is a conjecture due to Oesterlé and Masser in 1985. It states that, for any infinitesimal 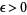, there exists a constant  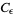such that for any three relatively prime integers 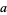, , 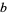 satisfying

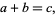(1)

the inequality

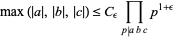(2)

holds, where 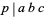 indicates that the product is over primes  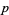which divide the product 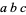. If this conjecture were true, it would imply Fermat's last theorem for sufficiently large powers (Goldfeld 1996). This is related to the fact that the abc conjecture implies that there are at least  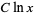non-Wieferich primes  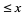for some constant  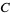(Silverman 1988, Vardi 1991).

The conjecture can also be stated by defining the height and radical of the sum 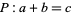 as

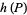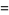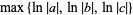			(3)
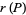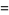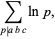			(4)

where 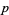 runs over all prime divisors of 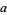, , 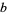and 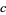. Then the abc conjecture states that for all 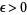, there exists a constant  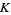such that for all ,

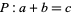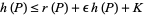(5)

(van Frankenhuysen 2000). van Frankenhuysen (2000) has shown that there exists an infinite sequence of sums  or rational integers with large height compared to the radical,

(6)

with

(7)

for 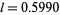, improving a result of Stewart and Tijdeman (1986).

REFERENCES:

Cox, D. A. "Introduction to Fermat's Last Theorem." Amer. Math. Monthly 101, 3-14, 1994.

Elkies, N. D. "ABC Implies Mordell." Internat. Math. Res. Not. 7, 99-109, 1991.

Goldfeld, D. "Beyond the Last Theorem." The Sciences 36, 34-40, March/April 1996.

Goldfeld, D. "Beyond the Last Theorem." Math. Horizons, 26-31 and 24, Sept. 1996.

Goldfeld, D. "Modular Forms, Elliptic Curves and the 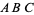-Conjecture." https://www.math.columbia.edu/~goldfeld/ABC-Conjecture.pdf.

Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 75-76, 1994.

Lang, S. "Old and New Conjectures in Diophantine Inequalities." Bull. Amer. Math. Soc. 23, 37-75, 1990.

Lang, S. Number Theory III: Diophantine Geometry. New York: Springer-Verlag, pp. 63-67, 1991.

Mason, R. C. Diophantine Equations over Functions Fields. Cambridge, England: Cambridge University Press, 1984.

Masser, D. W. "On 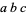 and Discriminants." Proc. Amer. Math. Soc. 130, 3141-3150, 2002.

Mauldin, R. D. "A Generalization of Fermat's Last Theorem: The Beal Conjecture and Prize Problem." Not. Amer. Math. Soc. 44, 1436-1437, 1997.

Nitaq, A. "The abc Conjecture Home Page." https://www.math.unicaen.fr/~nitaj/abc.html.

Oesterlé, J. "Nouvelles approches du 'théorème' de Fermat." Astérisque 161/162, 165-186, 1988.

Peterson, I. "MathTrek: The Amazing ABC Conjecture." Dec. 8, 1997. https://www.maa.org/mathland/mathtrek_12_8.html.

Silverman, J. "Wieferich's Criterion and the abc Conjecture." J. Number Th. 30, 226-237, 1988.

Stewart, C. L. and Tijdeman, R. "On the Oesterlé-Masser Conjecture." Mh. Math. 102, 251-257, 1986.

Stewart, C. L. and Yu, K. "On the ABC Conjecture." Math. Ann. 291, 225-230, 1991.

van Frankenhuysen, M. "The ABC Conjecture Implies Roth's Theorem and Mordell's Conjecture." Mat. Contemp. 16, 45-72, 1999.

van Frankenhuysen, M. "A Lower Bound in the abc Conjecture." J. Number Th. 82, 91-95, 2000.

Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 66, 1991.

Vojta, P. Diophantine Approximations and Value Distribution Theory. Berlin: Springer-Verlag, p. 84, 1987.