


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-1-2021
Date: 18-11-2019
Date: 1-12-2020
|
The first few terms in the continued fraction of the Champernowne constant are [0; 8, 9, 1, 149083, 1, 1, 1, 4, 1, 1, 1, 3, 4, 1, 1, 1, 15, 45754...10987, 6, 1, 1, 21, ...] (OEIS A030167), and the number of decimal digits in these terms are 0, 1, 1, 1, 6, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 166, 1, ... (OEIS A143532). E. W. Weisstein computed 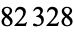 terms of the continued fraction on Jun. 30, 2013 using the Wolfram Language.
terms of the continued fraction on Jun. 30, 2013 using the Wolfram Language.
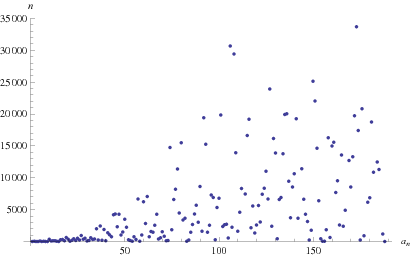
First occurrences of the terms 1, 2, 3, ... in the continued fraction ![[0;a_1,a_2,...,a_n]](http://mathworld.wolfram.com/images/equations/ChampernowneConstantContinuedFraction/Inline2.gif) occur at
occur at 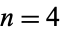 , 28, 13, 9, 93, 20, 31, 2, 3, 339, 71, 126, 107, ... (OEIS A038706). The smallest unknown value is 188, which has
, 28, 13, 9, 93, 20, 31, 2, 3, 339, 71, 126, 107, ... (OEIS A038706). The smallest unknown value is 188, which has 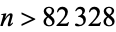 .
.
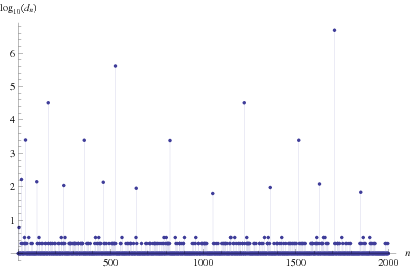
The continued fraction contains sporadic very large terms, making the continued fraction difficult to calculate. However, the size of the continued fraction high-water marks display apparent patterns (Sikora 2012). Large terms greater than 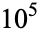 occur at positions 5, 19, 41, 102, 163, 247, 358, 460, ... and have 6, 166, 2504, 140, 33102, 109, 2468, 136, ... digits, respectively.
occur at positions 5, 19, 41, 102, 163, 247, 358, 460, ... and have 6, 166, 2504, 140, 33102, 109, 2468, 136, ... digits, respectively.
The high-water marks in terms of the continued fraction occur for terms 0, 1, 2, 4, 18, 40, 162, 526, 1708, 4838, 13522, 34062, ... (OEIS A143533; Sikora 2012), which have 0, 1, 1, 6, 166, 2504, 33102, 411100, 4911098, 57111096, 651111094, 7311111092, ... (OEIS A143534; Sikora 2012) decimal digits, respectively. Sikora (2012) conjectured that the number of decimal digits in the 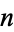 th high-water mark for
th high-water mark for 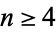 are given by
are given by
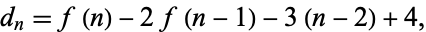 |
(1) |
where
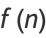 |
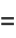 |
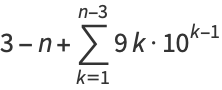 |
(2) |
 |
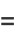 |
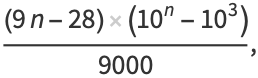 |
(3) |
in agreement with known calculated values up to 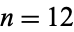 .
.
REFERENCES:
Havermann, H. "Numbers of Digits in Some Champernowne-Continued-Fraction Terms." http://odo.ca/~haha/cfcd.html.
Rytin, M. "Champernowne Constant and Its Continued Fraction Expansion." http://library.wolfram.com/infocenter/MathSource/2876/.
Sikora, J. K. "On the High Water Mark Convergents of Champernowne's Constant in Base Ten." 3 Oct 2012. http://arxiv.org/abs/1210.1263.
Sloane, N. J. A. Sequences A030167, A030190, A033307, A038706, A054635, A058935, A066716, A066717, A077771, A077772, A143532, A143533, and A143534 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|