Twin Primes

Twin primes are pairs of primes of the form (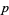, 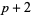). The term "twin prime" was coined by Paul Stäckel (1862-1919; Tietze 1965, p. 19). The first few twin primes are  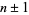for 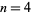, 6, 12, 18, 30, 42, 60, 72, 102, 108, 138, 150, 180, 192, 198, 228, 240, 270, 282, ... (OEIS A014574). Explicitly, these are (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), ... (OEIS A001359 and A006512).

All twin primes except (3, 5) are of the form .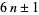

It is conjectured that there are an infinite number of twin primes (this is one form of the twin prime conjecture), but proving this remains one of the most elusive open problems in number theory. An important result for twin primes is Brun's theorem, which states that the number obtained by adding the reciprocals of the odd twin primes,

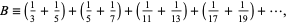(1)

converges to a definite number ("Brun's constant"), which expresses the scarcity of twin primes, even if there are infinitely many of them (Ribenboim 1996, p. 201). By contrast, the series of all prime reciprocals diverges to infinity, as follows from the Mertens second theorem by letting .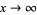

The following table gives the first few 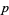 for the twin primes (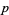, 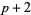), cousin primes (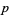, 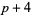), sexy primes (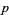, 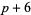), etc.

pair	OEIS	first member
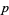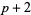(, )	A001359	3, 5, 11, 17, 29, 41, 59, 71, ...
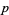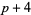(, )	A023200	3, 7, 13, 19, 37, 43, 67, 79, ...
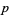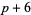(, )	A023201	5, 7, 11, 13, 17, 23, 31, 37, ...
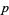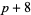(, )	A023202	3, 5, 11, 23, 29, 53, 59, 71, ...
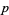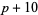(, )	A023203	3, 7, 13, 19, 31, 37, 43, 61, ...
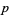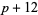(, )	A046133	5, 7, 11, 17, 19, 29, 31, 41, ...

Let 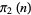 be the number of twin primes  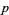and 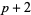 such that 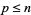. It is not known if there are an infinite number of such primes (Wells 1986, p. 41; Shanks 1993), but it seems almost certain to be true (Hardy and Wright 1979, p. 5).

J. R. Chen has shown there exists an infinite number of primes 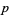 such that  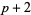has at most two factors (Le Lionnais 1979, p. 49). Brun proved that there exists a computable integer  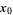such that if 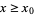, then

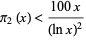(2)

(Ribenboim 1996, p. 261). It has been shown that

(3)

written more concisely as

(4)

where 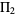 is known as the twin primes constant and  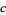is another constant. The constant  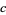has been reduced to  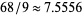(Fouvry and Iwaniec 1983),  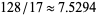(Fouvry 1984), 7 (Bombieri et al. 1986), 6.9075 (Fouvry and Grupp 1986), 6.8354 (Wu 1990), and 6.8325 (Haugland 1999). The latter calculation involved evaluation of 7-fold integrals and fitting of three different parameters.

Hardy and Littlewood (1923) conjectured that 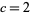 (Ribenboim 1996, p. 262), and that  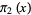is asymptotically equal to

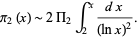(5)

This result is sometimes called the strong twin prime conjecture and is a special case of the k-tuple conjecture. A necessary (but not sufficient) condition for the twin prime conjecture to hold is that the prime gaps constant, defined by

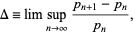(6)

where 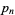 is the 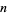th prime and  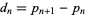is the prime difference function, satisfies .

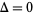Wolf notes that the formula

(7)

(which has asymptotic growth 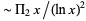) agrees with numerical data much better than does 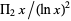, although not as well as .

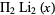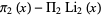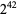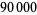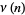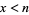Extending the search done by Brent in 1974 or 1975, Wolf has searched for the analog of the Skewes number for twins, i.e., an  such that  changes sign. Wolf checked numbers up to  and found more than  sign changes. From this data, Wolf conjectured that the number of sign changes  for  of 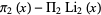 is given by

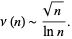(8)

Proof of this conjecture would also imply the existence an infinite number of twin primes.

The largest known twin primes as of Sep. 2016 correspond to

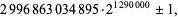(9)

each having 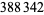 decimal digits and found by PrimeGrid on Dec. 25, 2011 (https://primes.utm.edu/top20/page.php?id=1#records).

In 1995, Nicely discovered a flaw in the Intel® PentiumTM microprocessor by computing the reciprocals of 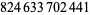 and 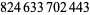, which should have been accurate to 19 decimal places but were incorrect from the tenth decimal place on (Cipra 1995, 1996; Nicely 1996).

If 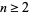, the integers  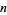and 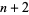 form a pair of twin primes iff

(10)

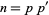 where 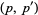 is a pair of twin primes iff

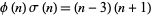(11)

(Ribenboim 1996, p. 259). S. M. Ruiz has found the unexpected result that 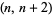 are twin primes iff

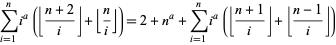(12)

for 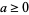, where  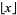is the floor function.

The values of 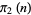 were found by Brent (1976) up to 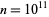. T. Nicely calculated them up to  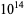in his calculation of Brun's constant. Fry et al. (2001) and Sebah (2002) independently obtained  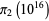using distributed computation. The following table gives known values of  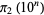(OEIS A007508; Ribenboim 1996, p. 263; Nicely 1999; Sebah 2002).

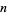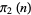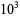	35
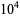	205
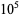	1224

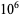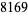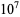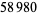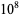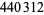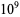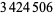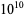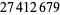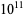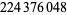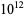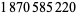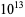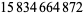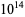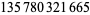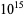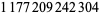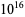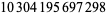It is conjectured that every even number is a sum of a pair of twin primes except a finite number of exceptions whose first few terms are 2, 4, 94, 96, 98, 400, 402, 404, 514, 516, 518, ... (OEIS A007534; Wells 1986, p. 132).

REFERENCES:

Bombieri, E.; Friedlander, J. B.; and Iwaniec, H. "Primes in Arithmetic Progression to Large Moduli." Acta Math. 156, 203-251, 1986.

Bradley, C. J. "The Location of Twin Primes." Math. Gaz. 67, 292-294, 1983.

Brent, R. P. "Irregularities in the Distribution of Primes and Twin Primes." Math. Comput. 29, 43-56, 1975.

Brent, R. P. "UMT 4." Math. Comput. 29, 221, 1975.

Brent, R. P. "Tables Concerning Irregularities in the Distribution of Primes and Twin Primes to 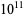." Math. Comput. 30, 379, 1976.

Caldwell, C. https://primes.utm.edu/top20/page.php?id=1.

Caldwell, C. K. "The Top Twenty: Twin Primes." https://www.utm.edu/research/primes/lists/top20/twin.html.

Cipra, B. "How Number Theory Got the Best of the Pentium Chip." Science 267, 175, 1995.

Cipra, B. "Divide and Conquer." What's Happening in the Mathematical Sciences, 1995-1996, Vol. 3. Providence, RI: Amer. Math. Soc., pp. 38-47, 1996.

Fouvry, É. "Autour du théorème de Bombieri-Vinogradov." Acta Math. 152, 219-244, 1984.

Fouvry, É. and Grupp, F. "On the Switching Principle in Sieve Theory." J. reine angew. Math. 370, 101-126, 1986.

Fouvry, É. and Iwaniec, H. "Primes in Arithmetic Progressions." Acta Arith. 42, 197-218, 1983.

Fry, P.; Nesheiwat, J.; and Szymanski, B. K. "Experiences with Distributed Computation of Twin Primes Distribution." In Progress in Computer Research, Vol. 2. (Ed. F. Columbus). Commack, NY: Nova Science Pub., pp. 187-203, 2001.

Gardner, M. "Patterns in Primes are a Clue to the Strong Law of Small Numbers." Sci. Amer. 243, 18-28, Dec. 1980.

Gourdon, X. and Sebah, P. "Introduction to Twin Primes and Brun's Constant Computation." https://numbers.computation.free.fr/Constants/Primes/twin.html.

Guy, R. K. "Gaps between Primes. Twin Primes." §A8 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 19-23, 1994.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.

Haugland, J. K. Application of Sieve Methods to Prime Numbers. Ph.D. thesis. Oxford, England: Oxford University, 1999.

Indlekofer, K. H. and Járai, A. "Largest Known Twin Primes." Math. Comput. 65, 427-428, 1996.

Indlekofer, K. H. and Járai, A. "Largest Known Twin Primes and Sophie Germain Primes." Math. Comput. 68, 1317-1324, 1999.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 46, 1979.

Nicely, T. R. "The Pentium Bug." https://www.trnicely.net/pentbug/pentbug.html.

Nicely, T. R. "Enumeration to 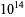 of the Twin Primes and Brun's Constant." Virginia J. Sci. 46, 195-204, 1996. https://www.trnicely.net/twins/twins.html.

Nicely, T. R. "New Maximal Prime Gaps and First Occurrences." Math. Comput. 68, 1311-1315, 1999.

Nyman, B. and Nicely, T. R. "New Prime Gaps Between 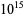 and 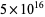." J. Int. Seq. 6, 1-6, 2003.

Parady, B. K.; Smith, J. F.; and Zarantonello, S. E. "Largest Known Twin Primes." Math. Comput. 55, 381-382, 1990.

Ribenboim, P. "Twin Primes." §4.3 in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 259-265, 1996.

Sebah, P. "Counting Twin Primes and Brun's Constant New Computation" 22 Aug 2002. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0208&L=nmbrthry&P=1968.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 30, 1993.

Sloane, N. J. A. Sequences A001359/M2476, A006512/M3763, A007508/M1855, A007534, and A014574 in "The On-Line Encyclopedia of Integer Sequences."

Tietze, H. "Prime Numbers and Prime Twins." Ch. 1 in Famous Problems of Mathematics: Solved and Unsolved Mathematics Problems from Antiquity to Modern Times. New York: Graylock Press, pp. 1-20, 1965.

Weintraub, S. "A Prime Gap of 864." J. Recr. Math. 25, 42-43, 1993.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 41, 1986.

Wolf, M. "On Twin and Cousin Primes." https://www.ift.uni.wroc.pl/~mwolf/.

Wolf, M. "Some Conjectures on the Gaps Between Consecutive Primes." https://www.ift.uni.wroc.pl/~mwolf/.

Wu, J. "Sur la suite des nombres premiers jumeaux." Acta. Arith. 55, 365-394, 1990.