


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-3-2020
Date: 14-7-2020
Date: 3-6-2020
|
A prime triplet is a prime constellation of the form (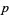 ,
, 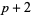 ,
, 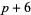 ), (
), (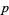 ,
, 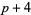 ,
, 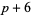 ), etc. Hardy and Wright (1979, p. 5) conjecture, and it seems almost certain to be true, that there are infinitely many prime triplets of the form (
), etc. Hardy and Wright (1979, p. 5) conjecture, and it seems almost certain to be true, that there are infinitely many prime triplets of the form (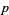 ,
, 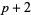 ,
, 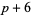 ) and (
) and (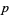 ,
, 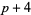 ,
, 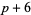 ).
).
| triplet | Sloane | first member |
(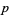 , , 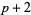 , , 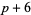 ) ) |
A022004 | 5, 11, 17, 41, 101, 107, ... |
(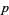 , , 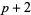 , , 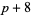 ) ) |
A046134 | 3, 5, 11, 29, 59, 71, 101, ... |
(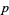 , , 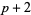 , , 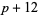 ) ) |
A046135 | 5, 11, 17, 29, 41, 59, 71, ... |
(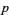 , , 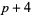 , , 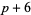 ) ) |
A022005 | 7, 13, 37, 67, 97, 103, ... |
(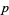 , , 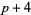 , , 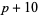 ) ) |
A046136 | 3, 7, 13, 19, 37, 43, 79, ... |
(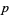 , , 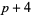 , , 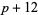 ) ) |
A046137 | 7, 19, 67, 97, 127, 229, ... |
(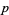 , , 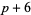 , , 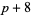 ) ) |
A046138 | 5, 11, 23, 53, 101, 131, ... |
(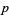 , , 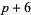 , , 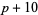 ) ) |
A046139 | 7, 13, 31, 37, 61, 73, 97, ... |
(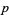 , , 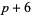 , , 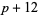 ) ) |
A023241 | 5, 7, 11, 17, 31, 41, 47, ... |
(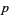 , , 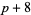 , , 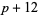 ) ) |
A046141 | 5, 11, 29, 59, 71, 89, 101, ... |
As of Apr. 2019, the largest known prime triplet of the form 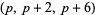 has smallest member
has smallest member
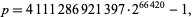 |
and each of its three members has 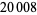 decimal digits.
decimal digits.
REFERENCES:
Forbes, T. "Prime 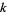 -Tuplets." https://anthony.d.forbes.googlepages.com/ktuplets.htm.
-Tuplets." https://anthony.d.forbes.googlepages.com/ktuplets.htm.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Rivera, C. "Problems & Puzzles: Puzzle 034-Prime Triplets in Arithmetic Progression." https://www.primepuzzles.net/puzzles/puzz_034.htm.
Sloane, N. J. A. Sequences A022004, A022005, A023241, A046134, A046135, A046136, A046137, A046138, A046139, and A046141in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|