Prime Gaps

A prime gap of length 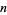 is a run of  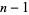consecutive composite numbers between two successive primes. Therefore, the difference between two successive primes  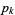and 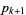 bounding a prime gap of length  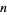is 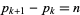, where  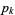is the 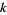th prime number. Since the prime difference function

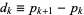(1)

is always even (except for 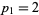), all primes gaps  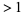are also even. The notation  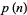is commonly used to denote the smallest prime  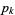corresponding to the start of a prime gap of length 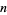, i.e., such that  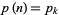is prime, 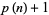, , 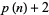...,  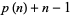are all composite, and  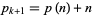is prime (with the additional constraint that no smaller number satisfying these properties exists).

The maximal prime gap 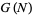 is the length of the largest prime gap that begins with a prime  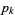less than some maximum value 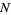. For 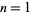, 2, ...,  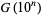is given by 4, 8, 20, 36, 72, 114, 154, 220, 282, 354, 464, 540, 674, 804, 906, 1132, ... (OEIS A053303).

Arbitrarily large prime gaps exist. For example, for any 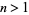, the numbers 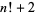, , 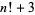...,  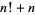are all composite (Havil 2003, p. 170). However, no general method more sophisticated than an exhaustive search is known for the determination of first occurrences and maximal prime gaps (Nicely 1999).

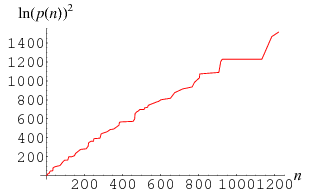
Cramér (1937) and Shanks (1964) conjectured that

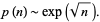(2)

Wolf conjectures a slightly different form

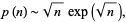(3)

which agrees better with numerical evidence.

Wolf conjectures that the maximal gap  between two consecutive primes less than 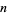 appears approximately at

(4)

where 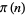 is the prime counting function and  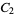is the twin primes constant. Setting  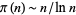reduces to Cramer's conjecture for large ,

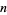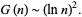(5)

It is known that there is a prime gap of length 803 following 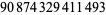, and a prime gap of length  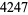following  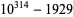(Baugh and O'Hara 1992). H. Dubner (2001) discovered a prime gap of length  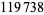between two 3396-digit probable primes. On Jan. 15, 2004, J. K. Andersen and H. Rosenthal found a prime gap of length  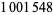between two probabilistic primes of  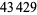digits each. In January-May 2004, Hans Rosenthal and Jens Kruse Andersen found a prime gap of length  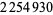between two probabilistic primes with  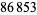digits each (Anderson 2004).

The merit of a prime gap compares the size of a gap to the local average gap, and is given by 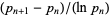. In 1999, the number 1693182318746371 was found, with merit 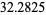. This remained the record merit until 804212830686677669 was found in 2005, with a gap of 1442 and a merit of 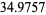. Andersen maintains a list of the top 20 known merits. The prime gaps of increasing merit are 2, 3, 7, 113, 1129, 1327, 19609, ... (OEIS A111870).

Young and Potler (1989) determined the first occurrences of prime gaps up to 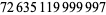, with all first occurrences found between 1 and 673. Nicely (1999) has extended the list of maximal prime gaps. The following table gives the values of  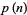for small 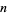, omitting degenerate runs which are part of a run with greater  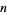(OEIS A005250 and A002386).

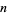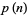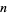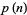1	2	354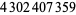
2	3	382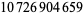
4	7	384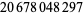
6	23	394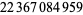
8	89	456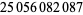
14	113	464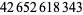
18	523	468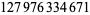
20	887	474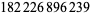
22		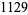486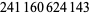
34		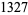490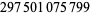
36		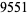500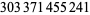
44		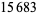514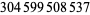
52		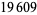516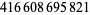
72		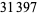532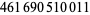
86		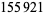534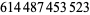
96		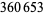540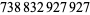
112		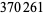582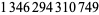
114		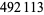588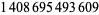
118		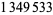602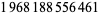
132		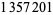652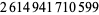
148		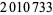674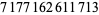
154		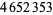716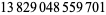
180		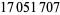766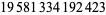
210		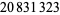778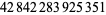
220		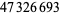804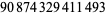
222		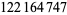806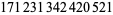
234		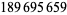906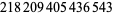
248		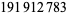916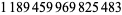
250		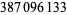924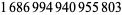
282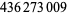
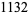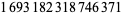288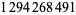
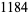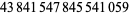292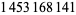
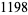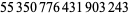320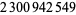
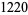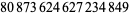336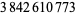

Define

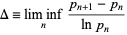(6)

as the infimum limit of the ratio of the 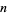th prime difference to the natural logarithm of the 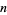th prime number. If there are an infinite number of twin primes, then 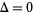. This follows since it must then be true that  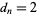infinitely often, say at  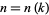for 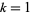, 2, ..., so a necessary condition for the twin prime conjecture to hold is that

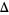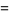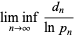			(7)
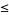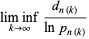			(8)
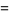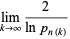			(9)
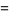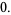			(10)

However, this condition is not sufficient, since the same proof works if 2 is replaced by any constant.

Hardy and Littlewood showed in 1926 that, subject to the truth of the generalized Riemann hypothesis, 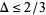. This was subsequently improved by Rankin (again assuming the generalized Riemann hypothesis) to 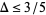. In 1940, Erdős used sieve theory to show for the first time with no assumptions that 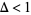. This was subsequently improved to 15/16 (Ricci),  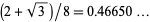(Bombieri and Davenport 1966), and  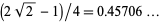(Pil'Tai 1972), as quoted in Le Lionnais (1983, p. 26). Huxley (1973, 1977) obtained 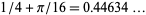, which was improved by Maier in 1986 to 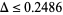, which was the best result known until 2003 (American Institute of Mathematics).

At a March 2003 meeting on elementary and analytic number theory in Oberwolfach, Germany, Goldston and Yildirim presented an attempted proof that 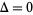. While the original proof turned out to be flawed (Mackenzie 2003ab), the result has now been established by a new proof (American Institute of Mathematics 2005, Cipra 2005, Devlin 2005, Goldston et al. 2005ab).

REFERENCES:

American Institute of Mathematics. "Small Gaps between Consecutive Primes: Recent Work of D. Goldston and C. Yildirim." https://www.aimath.org/goldston_tech/.

American Institute of Mathematics. "Breakthrough in Prime Number Theory." May 24, 2005. https://aimath.org/.

Andersen, J. K. "First Known Prime Megagap." https://hjem.get2net.dk/jka/math/primegaps/megagap.htm.

Andersen, J. K. "Largest Known Prime Gap." https://hjem.get2net.dk/jka/math/primegaps/megagap2.htm.

Andersen, J. K. "A Prime Gap of 1001548." 15 Jan 2004. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0401&L=nmbrthry&F=&S=&P=397.

Andersen, J. K. "A Prime Gap of 2254930." 2 Jun 2004. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0406&L=nmbrthry&P=601.

Andersen, J. K. "Top-20 Prime Gaps." https://hjem.get2net.dk/jka/math/primegaps/gaps20.htm.

Baugh, D. and O'Hara, F. "Large Prime Gaps." J. Recr. Math. 24, 186-187, 1992.

Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 133-134, 1994.

Bombieri, E. and Davenport, H. "Small Differences between Prime Numbers." Proc. Roy. Soc. A 293, 1-18, 1966.

Brent, R. P. "The First Occurrence of Large Gaps between Successive Primes." Math. Comput. 27, 959-963, 1973.

Brent, R. P. "The Distribution of Small Gaps between Successive Primes." Math. Comput. 28, 315-324, 1974.

Brent, R. P. "The First Occurrence of Certain Large Prime Gaps." Math. Comput. 35, 1435-1436, 1980.

Caldwell, C. "The Gaps Between Primes." https://primes.utm.edu/notes/gaps.html.

Cipra, B. "Proof Promises Progress in Prime Progressions." Science 304, 1095, 2004.

Cipra, B. "Third Time Proves Charm for Prime-Gap Theorem." Science 308, 1238, 2005.

Cramér, H. "On the Order of Magnitude of the Difference between Consecutive Prime Numbers." Acta Arith. 2, 23-46, 1937.

Cutter, P. A. "Finding Prime Pairs with Particular Gaps." Math. Comput. 70, 1737-1744, 2001.

Devlin, K. "Major Advance on the Twin Primes Conjecture." May 24, 2005. https://www.maa.org/news/052505twinprimes.html.

Dubner, H. "New Large Prime Gap Record." 13 Dec 2001. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0112&L=nmbrthry&P=1093.

Fouvry, É. "Autour du théorème de Bombieri-Vinogradov." Acta. Math. 152, 219-244, 1984.

Fouvry, É. and Grupp, F. "On the Switching Principle in Sieve Theory." J. reine angew. Math. 370, 101-126, 1986.

Fouvry, É. and Iwaniec, H. "Primes in Arithmetic Progression." Acta Arith. 42, 197-218, 1983.

Goldston, D. A.; Graham, S. W.; Pintz, J.; and Yildirim, C. Y. "Small Gaps between Primes or Almost Primes." Jun. 3, 2005a. https://www.arxiv.org/abs/math.NT/0506067/.

Goldston, D. A.; Motohashi, Y.; Pintz, J.; and Yildirim, C. Y. "Small Gaps between Primes Exist." May 14, 2005b. https://www.arxiv.org/abs/math.NT/0505300/.

Guy, R. K. "Gaps between Primes. Twin Primes" and "Increasing and Decreasing Gaps." §A8 and A11 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 19-23 and 26-27, 1994.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Huxley, M. N. "Small Differences between Consecutive Primes." Mathematica 20, 229-232, 1973.

Huxley, M. N. "Small Differences between Consecutive Primes. II." Mathematica 24, 142-152, 1977.

Lander, L. J. and Parkin, T. R. "On First Appearance of Prime Differences." Math. Comput. 21, 483-488, 1967.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, 1983.

Mackenzie, D. "Prime Proof Helps Mathematicians Mind the Gaps." Science 300, 32, 2003a.

Mackenzie, D. "Prime-Number Proof's Leap Falls Short." Science 300, 1066, 2003b.

Montgomery, H. "Small Gaps Between Primes." 13 Mar 2003. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0303&L=nmbrthry&P=1323.

Nicely, T. R. "First Occurrence Prime Gaps." https://www.trnicely.net/gaps/gaplist.html.

Nicely, T. R. "New Maximal Prime Gaps and First Occurrences." Math. Comput. 68, 1311-1315, 1999. https://www.trnicely.net/gaps/gaps.html.

Nicely, T. R. and Nyman, B. "First Occurrence of a Prime Gap of 1000 or Greater." https://www.trnicely.net/gaps/gaps2.html.

Nyman, B. and Nicely, T. R. "New Prime Gaps Between 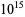 and 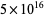." J. Int. Seq. 6, 1-6, 2003.

Rivera, C. "Problems & Puzzles: Puzzle 011-Distinct, Increasing & Decreasing Gaps." https://www.primepuzzles.net/puzzles/puzz_011.htm.

Shanks, D. "On Maximal Gaps between Successive Primes." Math. Comput. 18, 646-651, 1964.

Sloane, N. J. A. Sequences A002386/M0858, A008996, A008950, A008995, A008996, A030296, A053303, and A111870 in "The On-Line Encyclopedia of Integer Sequences."

Soundararajan, K. "Small Gaps Between Prime Numbers: The Work of Goldston-Pintz-Yildirim." Bull. Amer. Math. Soc. 44, 1-18, 2007.

Wolf, M. "First Occurrence of a Given Gap between Consecutive Primes." https://www.ift.uni.wroc.pl/~mwolf/.

Wolf, M. "Some Conjectures on the Gaps Between Consecutive Primes." https://www.ift.uni.wroc.pl/~mwolf/.

Young, J. and Potler, A. "First Occurrence Prime Gaps." Math. Comput. 52, 221-224, 1989.