


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-11-2019
Date: 15-11-2020
Date: 20-11-2020
|
If a number fails Miller's primality test for some base 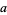 , it is not a prime. If the number passes, it may be a prime. A composite number passing Miller's test is called a strong pseudoprime to base
, it is not a prime. If the number passes, it may be a prime. A composite number passing Miller's test is called a strong pseudoprime to base 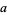 . If a number
. If a number 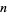 does not pass the test, then it is called a witness for the compositeness. If
does not pass the test, then it is called a witness for the compositeness. If 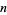 is an odd, positive composite number, then
is an odd, positive composite number, then 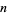 passes Miller's test for at most
passes Miller's test for at most 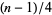 bases with
bases with 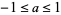 (Long 1995). There is no analog of Carmichael numbers for strong pseudoprimes.
(Long 1995). There is no analog of Carmichael numbers for strong pseudoprimes.
The smallest numbers that are strong pseudoprimes to base 2, 3, 5, and 7 (and would hence fail a test based on these bases) are 3215031751, 118670087467, 307768373641, 315962312077, ... (OEIS A074773; Jaeschke 1993).
Miller showed that any composite 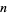 has a witness less than
has a witness less than 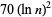 if the Riemann hypothesis is true.
if the Riemann hypothesis is true.
REFERENCES:
Caldwell, C. "Finding Primes & Proving Primality. 2.3: Strong Probable-Primality and a Practical Test." https://primes.utm.edu/prove/prove2_3.html.
Jaeschke, G. "On Strong Pseudoprimes to Several Bases." Math. Comput. 61, 915-926, 1993.
Long, C. T. Th. 4.21 in Elementary Introduction to Number Theory, 3rd ed. Prospect Heights, IL: Waveland Press, 1995.
Miller, G. "Riemann's Hypothesis and Tests for Primality." J. Comput. System Sci. 13, 300-317, 1976.
Sloane, N. J. A. Sequence A074773 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|