Münchhausen Number

A Münchhausen number (sometimes spelled Münchausen number, with a single 'h') is a number equal to the sum of its digits raised to each digit's power. Münchhausen numbers therefore differ from narcissistic numbers, which are numbers that equal the sum of a fixed power (in particular, the number of decimal digits) of the given number. The name "Münchhausen number" derives from the fact that these numbers "raise themselves" analogously to way in which Baron Hieronymus von Münchhausen allegedly raised himself by riding a cannonball, as portrayed in the 1943 fantasy comedy film Münchhausen.

If 0s are disallowed (since 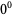 is not well-defined), the only Münchhausen numbers are 1 and

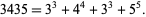If the definition 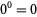 is adopted, then there are exactly four Münchhausen numbers: 0, 1, 3435, and 438579088 (OEIS A046253).

REFERENCES:

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 163-175, 1979.

Pickover, C. A. Keys to Infinity. New York: Wiley, pp. 169-171, 1995.

Pickover, C. A. Wonders of Numbers: Adventures in Mathematics, Mind, and Meaning. Oxford, England: Oxford University Press, 2001.

Sloane, N. J. A. Sequence A046253 in "The On-Line Encyclopedia of Integer Sequences."

van Berkel, D. "On a Curious Property of 3435." https://arxiv.org/pdf/0911.3038v2. Nov. 18, 2009.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 169 and 190, 1988.