


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-11-2019
Date: 30-10-2019
Date: 5-1-2020
|
The word "base" in mathematics is used to refer to a particular mathematical object that is used as a building block. The most common uses are the related concepts of the number system whose digits are used to represent numbers and the number system in which logarithms are defined. It can also be used to refer to the bottom edge or surface of a geometric figure.
A real number  can be represented using any integer number
can be represented using any integer number 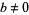 as a base (sometimes also called a radix or scale). The choice of a base yields to a representation of numbers known as a number system. In base
as a base (sometimes also called a radix or scale). The choice of a base yields to a representation of numbers known as a number system. In base 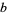 , the digits 0, 1, ...,
, the digits 0, 1, ..., 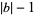 are used (where, by convention, for bases larger than 10, the symbols A, B, C, ... are generally used as symbols representing the decimal numbers 10, 11, 12, ...).
are used (where, by convention, for bases larger than 10, the symbols A, B, C, ... are generally used as symbols representing the decimal numbers 10, 11, 12, ...).
The digits of a number  in base
in base 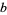 (for integer
(for integer 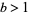 ) can be obtained in the Wolfram Language using IntegerDigits[x, b].
) can be obtained in the Wolfram Language using IntegerDigits[x, b].
Let the base 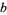 representation of a number
representation of a number  be written
be written
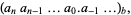 |
(1) |
(e.g., 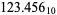 ). Then, for example, the number 10 is written in various bases as
). Then, for example, the number 10 is written in various bases as
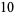 |
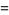 |
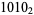 |
(2) |
 |
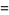 |
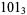 |
(3) |
 |
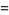 |
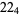 |
(4) |
 |
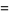 |
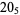 |
(5) |
 |
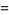 |
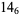 |
(6) |
 |
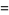 |
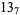 |
(7) |
 |
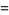 |
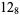 |
(8) |
 |
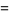 |
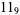 |
(9) |
 |
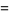 |
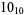 |
(10) |
 |
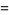 |
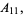 |
(11) |
since, for example,
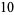 |
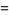 |
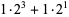 |
(12) |
 |
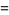 |
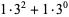 |
(13) |
 |
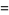 |
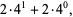 |
(14) |
and so on.
Common bases are given special names based on the value of 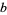 , as summarized in the following table. The most common bases are binary and hexadecimal (used by computers) and decimal (used by people).
, as summarized in the following table. The most common bases are binary and hexadecimal (used by computers) and decimal (used by people).
| base | number system |
| 2 | binary |
| 3 | ternary |
| 4 | quaternary |
| 5 | quinary |
| 6 | senary |
| 7 | septenary |
| 8 | octal |
| 9 | nonary |
| 10 | decimal |
| 11 | undenary |
| 12 | duodecimal |
| 16 | hexadecimal |
| 20 | vigesimal |
| 60 | sexagesimal |
The index of the leading digit needed to represent the number is
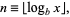 |
(15) |
where 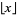 is the floor function. Now, recursively compute the successive digits
is the floor function. Now, recursively compute the successive digits
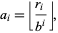 |
(16) |
where 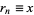 and
and
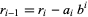 |
(17) |
for 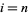 ,
, 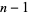 , ..., 1, 0, .... This gives the base
, ..., 1, 0, .... This gives the base 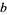 representation of
representation of  . Note that if
. Note that if  is an integer, then
is an integer, then 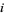 need only run through 0, and that if
need only run through 0, and that if  has a fractional part, then the expansion may or may not terminate. For example, the hexadecimal representation of 0.1 (which terminates in decimal notation) is the infinite expression
has a fractional part, then the expansion may or may not terminate. For example, the hexadecimal representation of 0.1 (which terminates in decimal notation) is the infinite expression 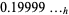 .
.
Some number systems use a mixture of bases for counting. Examples include the Mayan calendar and the old British monetary system (in which ha'pennies, pennies, threepence, sixpence, shillings, half crowns, pounds, and guineas corresponded to units of 1/2, 1, 3, 6, 12, 30, 240, and 252, respectively).
Bergman (1957/58) considered an irrational base, and Knuth (1998) considered transcendental bases. This leads to some rather unfamiliar results, such as equating 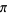 to 1 in "base
to 1 in "base 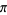 ,"
," 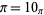 . Even more unexpectedly, the representation of a given integer in an irrational base may be nonunique, for example
. Even more unexpectedly, the representation of a given integer in an irrational base may be nonunique, for example
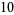 |
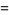 |
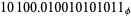 |
(18) |
 |
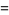 |
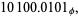 |
(19) |
where 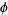 is the golden ratio.
is the golden ratio.
It is also possible to consider negative bases such as negabinary and negadecimal (e.g., Allouche and Shallit 2003). The digits in a negative base may be obtained with the Wolfram Language code
NegativeIntegerDigits[0, n_Integer?Negative] := {0}
NegativeIntegerDigits[i_, n_Integer?Negative] :=
Rest @ Reverse @ Mod[
NestWhileList[(# - Mod[#, -n])/n& ,
i, # != 0& ],
-n]
The base of a logarithm is a number 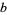 used to define the number system in which the logarithm is computed. In general, the logarithm of a number
used to define the number system in which the logarithm is computed. In general, the logarithm of a number  in base
in base 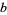 is written
is written 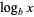 . The symbol
. The symbol 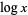 is an abbreviation regrettably used both for the common logarithm
is an abbreviation regrettably used both for the common logarithm 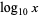 (by engineers and physicists and indicated on pocket calculators) and for the natural logarithm
(by engineers and physicists and indicated on pocket calculators) and for the natural logarithm 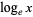 (by mathematicians).
(by mathematicians). 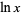 denotes the natural logarithm
denotes the natural logarithm 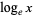 (as used by engineers and physicists and indicated on pocket calculators), and
(as used by engineers and physicists and indicated on pocket calculators), and 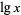 denotes
denotes 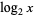 . In this work, the notations
. In this work, the notations 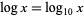 and
and 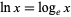 are used.
are used.
To convert between logarithms in different bases, the formula
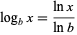 |
(20) |
can be used.
REFERENCES:
Allouche, J.-P. and Shallit, J. "Representations in Negative Bases." §3.7 in Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, pp. 103-105, 2003.
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 28, 1972.
Bergman, G. "A Number System with an Irrational Base." Math. Mag. 31, 98-110, 1957/58.
Bogomolny, A. "Base Converter." http://www.cut-the-knot.org/binary.shtml.
Knuth, D. E. "Positional Number Systems." §4.1 in The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, pp. 195-213, 1998.
Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 6-11, 1991.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|