


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-4-2020
Date: 5-9-2020
Date: 7-11-2020
|
Let 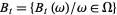 ,
, 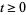 , be one-dimensional Brownian motion. Integration with respect to
, be one-dimensional Brownian motion. Integration with respect to 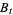 was defined by Itô (1951). A basic result of the theory is that stochastic integral equations of the form
was defined by Itô (1951). A basic result of the theory is that stochastic integral equations of the form
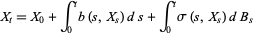 |
(1) |
can be interpreted as stochastic differential equations of the form
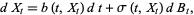 |
(2) |
where differentials are handled with the use of Itô's formula
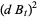 |
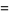 |
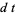 |
(3) |
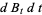 |
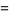 |
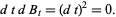 |
(4) |
Hudson and Parthasarathy (1984) obtained a Fock space representation of Brownian motion and Poisson processes. The boson Fock space 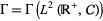 over
over 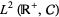 is the Hilbert space completion of the linear span of the exponential vectors
is the Hilbert space completion of the linear span of the exponential vectors 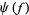 under the inner product
under the inner product
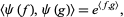 |
(5) |
where 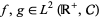 and
and 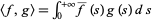 and
and 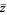 is the complex conjugate of
is the complex conjugate of 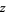 .
.
The annihilation, creation and conservation operators 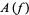 ,
, 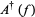 and
and 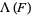 respectively, are defined on the exponential vectors
respectively, are defined on the exponential vectors 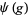 of
of 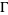 as follows,
as follows,
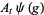 |
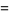 |
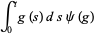 |
(6) |
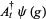 |
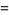 |
![partial/(partialepsilon)|_(epsilon=0)psi(g+epsilonchi_([0,t]))](https://mathworld.wolfram.com/images/equations/QuantumStochasticCalculus/Inline27.gif) |
(7) |
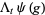 |
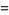 |
![partial/(partialepsilon)|_(epsilon=0)psi(e^(epsilonchi_([0,t])))g).](https://mathworld.wolfram.com/images/equations/QuantumStochasticCalculus/Inline30.gif) |
(8) |
The basic quantum stochastic differentials 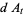 ,
, 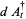 , and
, and 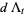 are defined as follows,
are defined as follows,
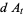 |
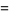 |
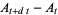 |
(9) |
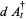 |
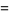 |
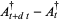 |
(10) |
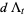 |
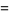 |
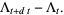 |
(11) |
Hudson and Parthasarathy (1984) defined stochastic integration with respect to the noise differentials of Definition 3 and obtained the Itô multiplication table
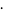 |
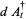 |
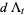 |
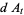 |
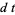 |
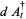 |
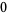 |
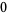 |
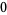 |
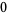 |
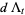 |
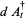 |
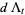 |
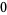 |
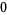 |
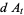 |
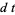 |
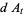 |
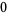 |
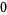 |
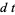 |
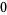 |
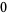 |
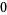 |
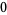 |
The two fundamental theorems of the Hudson-Parthasarathy quantum stochastic calculus give formulas for expressing the matrix elements of quantum stochastic integrals in terms of ordinary Lebesgue integrals. The first theorem states that is
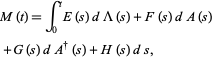 |
(12) |
where 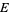 ,
, 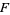 ,
, 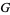 ,
, 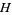 are (in general) time-dependent adapted processes. Let also
are (in general) time-dependent adapted processes. Let also 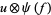 and
and 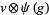 be in the exponential domain of
be in the exponential domain of 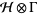 , then
, then
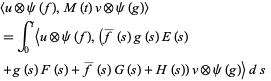 |
(13) |
The second theorem states that if
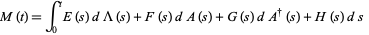 |
(14) |
and
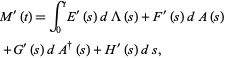 |
(15) |
where 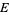 ,
, 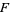 ,
, 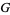 ,
, 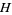 ,
, 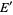 ,
, 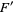 ,
, 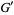 ,
, 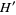 are (in general) time dependent adapted processes and also
are (in general) time dependent adapted processes and also 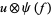 and
and 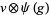 be in the exponential domain of
be in the exponential domain of 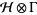 , then
, then
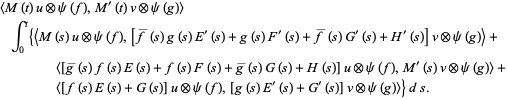 |
(16) |
The fundamental result that connects classical with quantum stochastics is that the processes 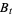 and
and 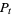 defined by
defined by
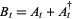 |
(17) |
and
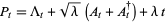 |
(18) |
are identified, through their statistical properties, e.g., their vacuum characteristic functionals
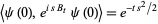 |
(19) |
and
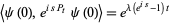 |
(20) |
with Brownian motion and a Poisson process of intensity 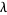 , respectively.
, respectively.
Within the framework of Hudson-Parthasarathy quantum stochastic calculus, classical quantum mechanical evolution equations take the form
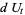 |
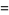 |
![-[(iH+1/2L^*L)dt+L^*WdA_t-LdA_t^|+(1-W)dLambda_t]U_t](https://mathworld.wolfram.com/images/equations/QuantumStochasticCalculus/Inline91.gif) |
(21) |
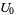 |
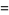 |
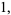 |
(22) |
where, for each 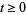 ,
, 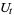 is a unitary operator defined on the tensor product
is a unitary operator defined on the tensor product 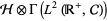 of a system Hilbert space
of a system Hilbert space 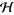 and the noise (or reservoir) Fock space
and the noise (or reservoir) Fock space 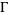 . Here,
. Here, 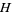 ,
, 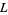 ,
, 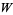 are in
are in 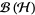 , the space of bounded linear operators on
, the space of bounded linear operators on 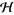 , with
, with 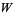 unitary and
unitary and 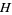 self-adjoint. Notice that for
self-adjoint. Notice that for 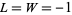 , equation (21) reduces to a classical stochastic differential equation of the form (2). Here and in what follows we identify time-independent, bounded, system space operators
, equation (21) reduces to a classical stochastic differential equation of the form (2). Here and in what follows we identify time-independent, bounded, system space operators 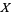 with their ampliation
with their ampliation 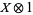 to
to 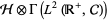 .
.
The quantum stochastic differential equation (analogue of the Heisenberg equation for quantum mechanical observables) satisfied by the quantum flow
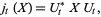 |
(23) |
where 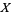 is a bounded system space operator, is
is a bounded system space operator, is
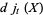 |
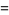 |
![j_t(i[H,X]-1/2(L^*LX+XL^*L-2L^*XL))dt+j_t([L^*,X]W)dA_t+j_t(W^*[X,L])dA_t^|+j_t(W^*XW-X)dLambda_t](https://mathworld.wolfram.com/images/equations/QuantumStochasticCalculus/Inline114.gif) |
(24) |
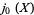 |
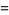 |
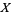 |
(25) |
for ![t in [0,T]](https://mathworld.wolfram.com/images/equations/QuantumStochasticCalculus/Inline118.gif) .
.
The commutation relations associated with the operator processes 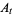 ,
, 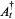 are the canonical (or Heisenberg) commutation relations, namely
are the canonical (or Heisenberg) commutation relations, namely
![[A_t,A_t^|]=tI.](https://mathworld.wolfram.com/images/equations/QuantumStochasticCalculus/NumberedEquation14.gif) |
(26) |
REFERENCES:
Hudson, R. L. and Parthasarathy, K. R. "Quantum Ito's Formula and Stochastic Evolutions." Comm. Math. Phys. 93, 301-323, 1984.
Itô, K. "On Stochastic Differential Equations." Mem. Amer. Math. Soc. No. 4, 1951.
Parthasarathy, K. R. An Introduction to Quantum Stochastic Calculus. Boston, MA: Birkhäuser, 1992.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|