
Brun,s Constant
 المؤلف:
Ball, W. W. R. and Coxeter, H. S. M.
المؤلف:
Ball, W. W. R. and Coxeter, H. S. M.
 المصدر:
Mathematical Recreations and Essays, 13th ed. New York: Dover,
المصدر:
Mathematical Recreations and Essays, 13th ed. New York: Dover,
 الجزء والصفحة:
...
الجزء والصفحة:
...
 5-9-2020
5-9-2020
 2480
2480
Brun's Constant
The number obtained by adding the reciprocals of the odd twin primes,
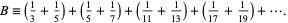 |
(1)
|
By Brun's theorem, the series converges to a definite number, which expresses the scarcity of twin primes, even if there are infinitely many of them (Ribenboim 1989, p. 201). By contrast, the series of all prime reciprocals diverges to infinity, as follows from the Mertens second theorem by letting 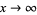 (which provides a stronger characterization of the divergence than Euler's proof that
(which provides a stronger characterization of the divergence than Euler's proof that 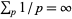 , obtained more than a century before Mertens' proof).
, obtained more than a century before Mertens' proof).
Shanks and Wrench (1974) used all the twin primes among the first 2 million numbers. Brent (1976) calculated all twin primes up to 100 billion and obtained (Ribenboim 1989, p. 146)
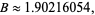 |
(2)
|
assuming the truth of the first Hardy-Littlewood conjecture. Using twin primes up to 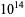 , Nicely (1996) obtained
, Nicely (1996) obtained
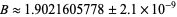 |
(3)
|
(Cipra 1995, 1996), in the process discovering a bug in Intel's® PentiumTM microprocessor. Using twin primes up to 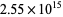 , Nicely (2000) subsequently obtained the result
, Nicely (2000) subsequently obtained the result
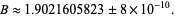 |
(4)
|
The number of terms has since been calculated using twin primes up to 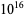 (Sebah 2002), giving the result
(Sebah 2002), giving the result
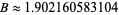 |
(5)
|
(OEIS A065421). Note that the value for 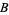 given by Le Lionnais (1983) is incorrect.
given by Le Lionnais (1983) is incorrect.
Segal (1930) proved that Brun-type sums 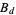 of
of 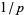 over consecutive primes separated by
over consecutive primes separated by 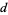 are convergent (Halberstam and Richert 1983, p. 92). Wolf suggests that
are convergent (Halberstam and Richert 1983, p. 92). Wolf suggests that 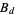 is roughly equal to
is roughly equal to 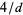 which, in the
which, in the 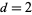 case of twin primes, gives
case of twin primes, gives 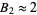 instead of
instead of 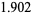 .... Wolf also considers the "cousin primes" Brun's constant
.... Wolf also considers the "cousin primes" Brun's constant 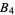 .
.
REFERENCES:
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 64, 1987.
Brent, R. P. "Tables Concerning Irregularities in the Distribution of Primes and Twin Primes Up to 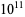 ." Math. Comput. 30, 379, 1976.
." Math. Comput. 30, 379, 1976.
Brun, V. "La serie 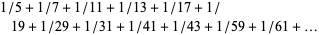 , les dénominateurs sont nombres premiers jumeaux est convergente où finie." Bull. Sci. Math. 43, 124-128, 1919.
, les dénominateurs sont nombres premiers jumeaux est convergente où finie." Bull. Sci. Math. 43, 124-128, 1919.
Cipra, B. "How Number Theory Got the Best of the Pentium Chip." Science 267, 175, 1995.
Cipra, B. "Divide and Conquer." What's Happening in the Mathematical Sciences, 1995-1996, Vol. 3. Providence, RI: Amer. Math. Soc., pp. 38-47, 1996.
Finch, S. R. "Brun's Constant." §2.14 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 133-135, 2003.
Gourdon, X. and Sebah, P. "Introduction to Twin Primes and Brun's Constant Computation." https://numbers.computation.free.fr/Constants/Primes/twin.html.
Halberstam, H. and Richert, H.-E. Sieve Methods. New York: Academic Press, 1983.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 30, 2003.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 41, 1983.
Nagell, T. Introduction to Number Theory. New York: Wiley, p. 67, 1951.
Nicely, T. "Enumeration to 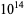 of the Twin Primes and Brun's Constant." Virginia J. Sci. 46, 195-204, 1996. https://www.trnicely.net/twins/twins.html.
of the Twin Primes and Brun's Constant." Virginia J. Sci. 46, 195-204, 1996. https://www.trnicely.net/twins/twins.html.
Nicely, T. "A New Error Analysis of Brun's Constant." Submitted to Virginia J. Sci., 2000. https://www.trnicely.net/twins/twins4.html.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1989.
Sebah, P. "Counting twin primes and Brun's constant new computation" 22 Aug 2002. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0208&L=NMBRTHRY&P=1968.
Segal, B. "Généralisation du théorème de Brun." Dokl. Akad. Nauk SSSR, 501-507, 1930.
Shanks, D. and Wrench, J. W. "Brun's Constant." Math. Comput. 28, 293-299, 1974.
Sloane, N. J. A. Sequence A065421 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 40-41, 1986.
Wolf, M. "Generalized Brun's Constants." https://www.ift.uni.wroc.pl/~mwolf/.
Wolf, M. "On Twin and Cousin Primes." https://www.ift.uni.wroc.pl/~mwolf/. 1996.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


