


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-7-2020
Date: 26-7-2020
Date: 13-1-2020
|
The 7.1.2 equation
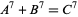 |
(1) |
is a special case of Fermat's last theorem with 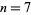 , and so has no solution. No solutions to the 7.1.3, 7.1.4, 7.1.5, 7.1.6 equations are known. There is now a known solutions to the 7.1.7 equation,
, and so has no solution. No solutions to the 7.1.3, 7.1.4, 7.1.5, 7.1.6 equations are known. There is now a known solutions to the 7.1.7 equation,
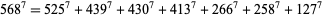 |
(2) |
(M. Dodrill 1999, PowerSum), requiring an update by Guy (1994, p. 140). The smallest 7.1.8 solution is
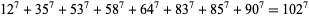 |
(3) |
(Lander et al. 1967, Ekl 1998). The smallest 7.1.9 solution is
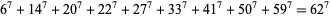 |
(4) |
(Lander et al. 1967).
No solutions to the 7.2.2, 7.2.3, 7.2.4, or 7.2.5 equations are known. The smallest 7.2.6 equation is
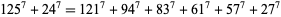 |
(5) |
(Meyrignac). The smallest 7.2.8 solution is
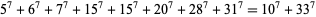 |
(6) |
(Lander et al. 1967, Ekl 1998). A 7.2.10.10 solution is
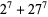 |
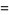 |
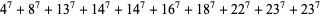 |
(7) |
 |
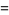 |
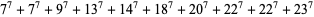 |
(8) |
(Lander et al. 1967).
No solutions to the 7.3.3 equation are known (Ekl 1996), nor are any to 7.3.4. The smallest 7.3.5 equations are
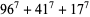 |
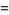 |
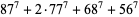 |
(9) |
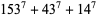 |
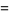 |
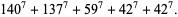 |
(10) |
No solutions are known to the 7.3.6 equation. The smallest 7.3.7 solution is
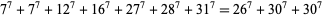 |
(11) |
(Lander et al. 1967).
Guy (1994, p. 140) asked if a 7.4.4 equation exists. The following solution provide an affirmative answer
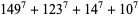 |
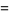 |
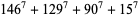 |
(12) |
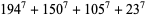 |
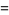 |
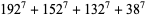 |
(13) |
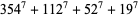 |
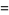 |
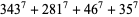 |
(14) |
(Ekl 1996, 1998; M. Lau 1999; PowerSum). Numerical solutions to the 7.4.5 equation are given by Gloden (1949). The smallest primitive 7.4.5 solutions are
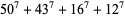 |
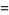 |
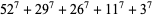 |
(15) |
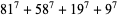 |
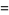 |
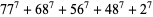 |
(16) |
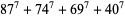 |
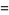 |
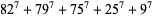 |
(17) |
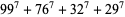 |
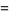 |
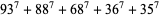 |
(18) |
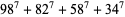 |
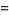 |
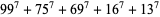 |
(19) |
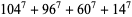 |
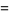 |
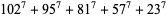 |
(20) |
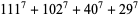 |
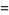 |
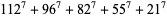 |
(21) |
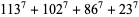 |
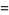 |
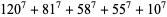 |
(22) |
(Lander et al. 1967, Ekl 1998).
Gloden (1949) gives parametric solutions to the 7.5.5 equation. The first few 7.5.5 solutions are
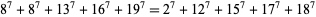 |
(23) |
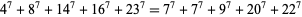 |
(24) |
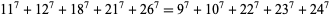 |
(25) |
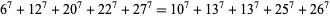 |
(26) |
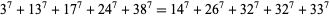 |
(27) |
(Lander et al. 1967). Ekl (1998) mentions but does not list 107 primitive solutions to 7.5.5.
A parametric solution to the 7.6.6 equation was given by Sastry and Rai (1948). The smallest is
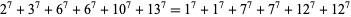 |
(28) |
(Lander et al. 1967). Another found by Chen Shuwen is
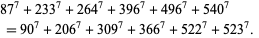 |
(29) |
Moessner and Gloden (1944) gave the 7.9.10 solution
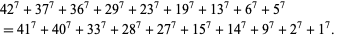 |
(30) |
REFERENCES:
Ekl, R. L. "Equal Sums of Four Seventh Powers." Math. Comput. 65, 1755-1756, 1996.
Ekl, R. L. "New Results in Equal Sums of Like Powers." Math. Comput. 67, 1309-1315, 1998.
Gloden, A. "Zwei Parameterlösungen einer mehrgeradigen Gleichung." Arch. Math. 1, 480-482, 1949.
Guy, R. K. "Sums of Like Powers. Euler's Conjecture." §D1 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-144, 1994.
Lander, L. J.; Parkin, T. R.; and Selfridge, J. L. "A Survey of Equal Sums of Like Powers." Math. Comput. 21, 446-459, 1967.
Meyrignac, J.-C. "Computing Minimal Equal Sums of Like Powers." https://euler.free.fr.
Moessner, A. and Gloden, A. "Einige Zahlentheoretische Untersuchungen und Resultate." Bull. Sci. École Polytech. de Timisoara 11, 196-219, 1944.
Nagell, T. "The Diophantine Equation 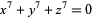 ." §67 in Introduction to Number Theory. New York: Wiley, pp. 248-251, 1951.
." §67 in Introduction to Number Theory. New York: Wiley, pp. 248-251, 1951.
Sastry, S. and Rai, T. "On Equal Sums of Like Powers." Math. Student 16, 18-19, 1948.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|