


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-8-2020
Date: 12-12-2020
Date: 10-4-2020
|
A primitive root of a prime 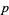 is an integer
is an integer 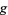 such that
such that 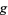 (mod
(mod 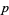 ) has multiplicative order
) has multiplicative order 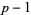 (Ribenboim 1996, p. 22). More generally, if
(Ribenboim 1996, p. 22). More generally, if 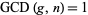 (
( and
and  are relatively prime) and
are relatively prime) and 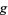 is of multiplicative order
is of multiplicative order 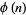 modulo
modulo 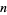 where
where 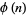 is the totient function, then
is the totient function, then 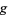 is a primitive root of
is a primitive root of 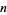 (Burton 1989, p. 187). The first definition is a special case of the second since
(Burton 1989, p. 187). The first definition is a special case of the second since 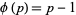 for
for 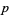 a prime.
a prime.
A primitive root of a number 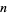 (but not necessarily the smallest primitive root for composite
(but not necessarily the smallest primitive root for composite 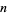 ) can be computed in the Wolfram Language using PrimitiveRoot[n].
) can be computed in the Wolfram Language using PrimitiveRoot[n].
If 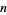 has a primitive root, then it has exactly
has a primitive root, then it has exactly 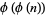 of them (Burton 1989, p. 188), which means that if
of them (Burton 1989, p. 188), which means that if 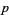 is a prime number, then there are exactly
is a prime number, then there are exactly 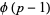 incongruent primitive roots of
incongruent primitive roots of 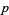 (Burton 1989). For
(Burton 1989). For 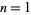 , 2, ..., the first few values of
, 2, ..., the first few values of 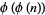 are 1, 1, 1, 1, 2, 1, 2, 2, 2, 2, 4, 2, 4, 2, 4, 4, 8, ... (OEIS A010554).
are 1, 1, 1, 1, 2, 1, 2, 2, 2, 2, 4, 2, 4, 2, 4, 4, 8, ... (OEIS A010554). 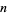 has a primitive root if it is of the form 2, 4,
has a primitive root if it is of the form 2, 4, 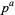 , or
, or 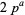 , where
, where 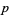 is an odd prime and
is an odd prime and 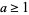 (Burton 1989, p. 204). The first few
(Burton 1989, p. 204). The first few 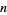 for which primitive roots exist are 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 17, 18, 19, 22, ... (OEIS A033948), so the number of primitive root of order
for which primitive roots exist are 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 17, 18, 19, 22, ... (OEIS A033948), so the number of primitive root of order 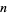 for
for 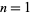 , 2, ... are 0, 1, 1, 1, 2, 1, 2, 0, 2, 2, 4, 0, 4, ... (OEIS A046144).
, 2, ... are 0, 1, 1, 1, 2, 1, 2, 0, 2, 2, 4, 0, 4, ... (OEIS A046144).
The smallest primitive roots for the first few primes 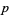 are 1, 2, 2, 3, 2, 2, 3, 2, 5, 2, 3, 2, 6, 3, 5, 2, 2, 2, ... (OEIS A001918). Here is table of the primitive roots for the first few
are 1, 2, 2, 3, 2, 2, 3, 2, 5, 2, 3, 2, 6, 3, 5, 2, 2, 2, ... (OEIS A001918). Here is table of the primitive roots for the first few 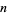 for which a primitive root exists (OEIS A046147).
for which a primitive root exists (OEIS A046147).
 |
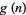 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 2, 3 |
| 6 | 5 |
| 7 | 3, 5 |
| 9 | 2, 5 |
| 10 | 3, 7 |
| 11 | 2, 6, 7, 8 |
| 13 | 2, 6, 7, 11 |
The largest primitive roots for 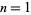 , 2, ..., are 0, 1, 2, 3, 3, 5, 5, 0, 5, 7, 8, 0, 11, ... (OEIS A046146). The smallest primitive roots for the first few integers
, 2, ..., are 0, 1, 2, 3, 3, 5, 5, 0, 5, 7, 8, 0, 11, ... (OEIS A046146). The smallest primitive roots for the first few integers 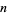 are given in the following table (OEIS A046145), which omits
are given in the following table (OEIS A046145), which omits 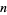 when
when 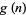 does not exist.
does not exist.
| 2 | 1 | 38 | 3 | 94 | 5 | 158 | 3 |
| 3 | 2 | 41 | 6 | 97 | 5 | 162 | 5 |
| 4 | 3 | 43 | 3 | 98 | 3 | 163 | 2 |
| 5 | 2 | 46 | 5 | 101 | 2 | 166 | 5 |
| 6 | 5 | 47 | 5 | 103 | 5 | 167 | 5 |
| 7 | 3 | 49 | 3 | 106 | 3 | 169 | 2 |
| 9 | 2 | 50 | 3 | 107 | 2 | 173 | 2 |
| 10 | 3 | 53 | 2 | 109 | 6 | 178 | 3 |
| 11 | 2 | 54 | 5 | 113 | 3 | 179 | 2 |
| 13 | 2 | 58 | 3 | 118 | 11 | 181 | 2 |
| 14 | 3 | 59 | 2 | 121 | 2 | 191 | 19 |
| 17 | 3 | 61 | 2 | 122 | 7 | 193 | 5 |
| 18 | 5 | 62 | 3 | 125 | 2 | 194 | 5 |
| 19 | 2 | 67 | 2 | 127 | 3 | 197 | 2 |
| 22 | 7 | 71 | 7 | 131 | 2 | 199 | 3 |
| 23 | 5 | 73 | 5 | 134 | 7 | 202 | 3 |
| 25 | 2 | 74 | 5 | 137 | 3 | 206 | 5 |
| 26 | 7 | 79 | 3 | 139 | 2 | 211 | 2 |
| 27 | 2 | 81 | 2 | 142 | 7 | 214 | 5 |
| 29 | 2 | 82 | 7 | 146 | 5 | 218 | 11 |
| 31 | 3 | 83 | 2 | 149 | 2 | 223 | 3 |
| 34 | 3 | 86 | 3 | 151 | 6 | 226 | 3 |
| 37 | 2 | 89 | 3 | 157 | 5 | 227 | 2 |
Let 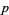 be any odd prime
be any odd prime 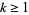 , and let
, and let
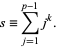 |
(1) |
Then
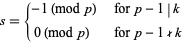 |
(2) |
(Ribenboim 1996, pp. 22-23). For numbers 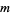 with primitive roots, all
with primitive roots, all 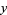 satisfying
satisfying 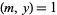 are representable as
are representable as
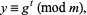 |
(3) |
where 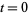 , 1, ...,
, 1, ..., 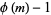 ,
, 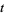 is known as the index, and
is known as the index, and 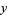 is an integer. Kearnes (1984) showed that for any positive integer
is an integer. Kearnes (1984) showed that for any positive integer 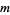 , there exist infinitely many primes
, there exist infinitely many primes 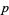 such that
such that
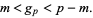 |
(4) |
Call the least primitive root 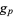 . Burgess (1962) proved that
. Burgess (1962) proved that
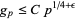 |
(5) |
for 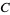 and
and 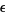 positive constants and
positive constants and 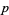 sufficiently large (Ribenboim 1996, p. 24).
sufficiently large (Ribenboim 1996, p. 24).
Matthews (1976) obtained a formula for the "two-dimensional" Artin's constants for the set of primes for which 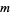 and
and 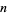 are both primitive roots.
are both primitive roots.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Primitive Roots." §24.3.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 827, 1972.
Burgess, D. A. "On Character Sums and 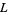 -Series." Proc. London Math. Soc. 12, 193-206, 1962.
-Series." Proc. London Math. Soc. 12, 193-206, 1962.
Burton, D. M. "The Order of an Integer Modulo 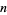 ," "Primitive Roots for Primes," and "Composite Numbers Having Primitive Roots." §8.1-8.3 in Elementary Number Theory, 4th ed. Dubuque, IA: William C. Brown Publishers, pp. 184-205, 1989.
," "Primitive Roots for Primes," and "Composite Numbers Having Primitive Roots." §8.1-8.3 in Elementary Number Theory, 4th ed. Dubuque, IA: William C. Brown Publishers, pp. 184-205, 1989.
Guy, R. K. "Primitive Roots." §F9 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 248-249, 1994.
Jones, G. A. and Jones, J. M. "Primitive Roots." §6.2 in Elementary Number Theory. Berlin: Springer-Verlag, pp. 99-103, 1998.
Kearnes, K. "Solution of Problem 6420." Amer. Math. Monthly 91, 521, 1984.
Lehmer, D. H. "A Note on Primitive Roots." Scripta Math. 26, 117-119, 1961.
Matthews, K. R. "A Generalization of Artin's Conjecture for Primitive Roots." Acta Arith. 29, 113-146, 1976.
Nagell, T. "Moduli Having Primitive Roots." §32 in Introduction to Number Theory. New York: Wiley, pp. 107-111, 1951.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 22-25, 1996.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, p. 97, 1994.
Sloane, N. J. A. Sequences A001918/M0242, A010554, and A033948 in "The On-Line Encyclopedia of Integer Sequences."
Western, A. E. and Miller, J. C. P. Tables of Indices and Primitive Roots. Cambridge, England: Cambridge University Press, pp. xxxvii-xlii, 1968.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|