


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-9-2020
Date: 24-10-2019
Date: 26-12-2019
|
 |
 |
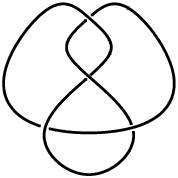
The figure eight knot, also known as the Flemish knot and savoy knot, is the unique prime knot of four crossings 04-001. It has braid word  .
.
The figure eight knot is implemented in the Wolfram Language as KnotData["FigureEight"].
It is a 2-embeddable knot, and is amphichiral as well as invertible. It has Arf invariant 1. It is not a slice knot (Rolfsen 1976, p. 224).
The Alexander polynomial  , BLM/Ho polynomial
, BLM/Ho polynomial  , Conway polynomial
, Conway polynomial  , HOMFLY polynomial
, HOMFLY polynomial  , Jones polynomial
, Jones polynomial  , and Kauffman polynomial F
, and Kauffman polynomial F  of the figure eight knot are
of the figure eight knot are
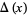 |
 |
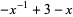 |
(1) |
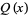 |
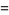 |
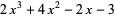 |
(2) |
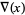 |
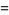 |
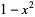 |
(3) |
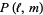 |
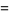 |
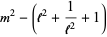 |
(4) |
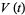 |
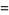 |
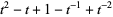 |
(5) |
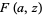 |
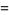 |
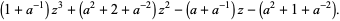 |
(6) |
There are no other knots on 10 or fewer crossings sharing the same Alexander polynomial, BLM/Ho polynomial, bracket polynomial, HOMFLY polynomial, Jones polynomial, or Kauffman polynomial F.
The figure eight knot has knot group
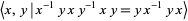 |
(7) |
(Rolfsen 1976, p. 58).

Helaman Ferguson's sculpture "Figure-Eight Complement II" illustrates the knot complement of the figure eight knot (Borwein and Bailey 2003, pp. 54-55, color plate IV, and front cover; Bailey et al. 2007, p. 37). Furthermore, Ferguson has carved the BBP-type formula for the hyperbolic volume of the knot complement (discussed below) on both figure eight knot complement sculptures commissioned by the Clay Mathematics Institute (Borwein and Bailey 2003, p. 56; Bailey et al. 2007, pp. 36-38).
The hyperbolic volume of the knot complement of the figure eight knot is approximately given by
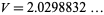 |
(8) |
(OEIS A091518). Exact expressions are given by the infinite sums
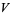 |
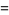 |
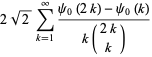 |
(9) |
 |
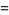 |
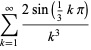 |
(10) |
 |
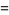 |
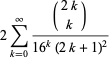 |
(11) |
 |
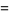 |
![(2pi)/3[1-ln(pi/3)+sum_(k=1)^(infty)(zeta(2k))/(k(2k+1)6^(2k))]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline37.gif) |
(12) |
 |
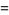 |
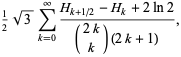 |
(13) |
where  is a harmonic number.
is a harmonic number.
 has a variety of BBP-type formulas including
has a variety of BBP-type formulas including
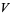 |
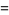 |
![sqrt(3)sum_(k=0)^(infty)[1/((3k+1)^2)-2/((3k+2)^2)+4/((3k+3)^2)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline45.gif) |
(14) |
 |
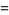 |
![(3sqrt(3))/2sum_(k=0)^(infty)[1/((3k+1)^2)-1/((3k+2)^2)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline48.gif) |
(15) |
 |
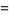 |
![sqrt(3)sum_(k=0)^(infty)[1/((6k+1)^2)+1/((6k+2)^2)-1/((6k+4)^2)-1/((6k+5)^2)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline51.gif) |
(16) |
 |
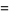 |
![sqrt(3)sum_(k=0)^(infty)[2/((6k+1)^2)-3/((6k+2)^2)-1/((6k+5)^2)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline54.gif) |
(17) |
 |
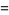 |
![sqrt(3)sum_(k=0)^(infty)[1/((6k+1)^2)+3/((6k+4)^2)-2/((6k+5)^2)],](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline57.gif) |
(18) |
with additional identities for coefficients of  of the form
of the form  (E. W. Weisstein, Sep. 30, 2007). Higher-order identities are
(E. W. Weisstein, Sep. 30, 2007). Higher-order identities are
![V=(2sqrt(3))/(243)sum_(k=0)^infty1/(729^k)[(243)/((12k+1)^2)-(243)/((12k+2)^2)-(324)/((12k+3)^2)-(81)/((12k+4)^2)+(27)/((12k+5)^2)-9/((12k+7)^2)+9/((12k+8)^2)
+(12)/((12k+9)^2)+3/((12k+10)^2)-1/((12k+11)^2)]
=(2sqrt(3))/(177147)sum_(k=0)^infty1/(531441^k)[(177147)/((24k+1)^2)-(177147)/((24k+2)^2)-(236196)/((24k+3)^2)-(59049)/((24k+4)^2)+(19683)/((24k+5)^2)-(6561)/((24k+7)^2)+(6561)/((24k+8)^2)+(8748)/((24k+9)^2)+(2187)/((24k+10)^2)-(729)/((24k+11)^2)+(243)/((24k+13)^2)-(243)/((24k+14)^2)-(324)/((24k+15)^2)-(81)/((24k+16)^2)+(27)/((24k+17)^2)-9/((24k+19)^2)+9/((24k+20)^2)+(12)/((24k+21)^2)+3/((24k+22)^2)
-1/((24k+23)^2)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/NumberedEquation3.gif) |
(19) |
(E. W. Weisstein, Aug. 11, 2008).
Additional classes of identities are given by
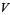 |
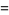 |
![sqrt(3)sum_(k=0)^(infty)(-1)^k[1/((3k+1)^2)+1/((3k+2)^2)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline62.gif) |
(20) |
 |
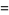 |
![sqrt(3)sum_(k=0)^(infty)(-1)^k[1/((9k+1)^2)+1/((9k+2)^2)-1/((9k+4)^2)-1/((9k+5)^2)+1/((9k+7)^2)+1/((9k+8)^2)],](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline65.gif) |
(21) |
with additional identities for coefficients of  of the form
of the form  (E. W. Weisstein, Sep. 30, 2007). Another BBP-type formula is given by
(E. W. Weisstein, Sep. 30, 2007). Another BBP-type formula is given by
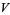 |
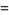 |
![(2sqrt(3))/9sum_(k=0)^(infty)((-1)^k)/(27^k)[9/((6k+1)^2)-9/((6k+2)^2)-(12)/((6k+3)^2)-3/((6k+4)^2)+1/((6k+5)^2)].](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline70.gif) |
(22) |
 is also given by the integrals
is also given by the integrals
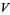 |
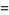 |
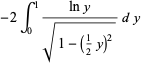 |
(23) |
 |
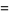 |
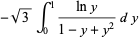 |
(24) |
 |
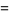 |
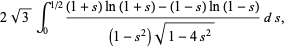 |
(25) |
and the analytic expressions
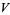 |
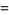 |
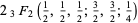 |
(26) |
 |
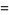 |
![1/6sqrt(3)[psi_1(1/3)-psi_1(2/3)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline86.gif) |
(27) |
 |
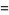 |
![1/9sqrt(3)[3psi_1(1/3)-2pi^2]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline89.gif) |
(28) |
 |
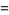 |
![1/(36)sqrt(3)[psi_1(1/6)+psi_1(1/3)-psi_1(2/3)-psi_1(5/6)]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline92.gif) |
(29) |
 |
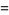 |
![i[Li_2(e^(-ipi/3))-Li_2(e^(ipi/3))]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline95.gif) |
(30) |
 |
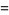 |
![2I[Li_2(e^(ipi/3))]](http://mathworld.wolfram.com/images/equations/FigureEightKnot/Inline98.gif) |
(31) |
 |
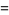 |
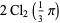 |
(32) |
 |
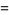 |
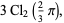 |
(33) |
(Broadhurst 1998; Borwein and Bailey 2003, pp. 54 and 88-92; Bailey et al. 2007, pp. 36-38 and 265-266), where  is a generalized hypergeometric function,
is a generalized hypergeometric function,  is the trigamma function,
is the trigamma function,  is the dilogarithm and
is the dilogarithm and  is Clausen's integral.
is Clausen's integral.
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Bar-Natan, D. "The Knot  ." http://www.math.toronto.edu/~drorbn/KAtlas/Knots/4.1.html.
." http://www.math.toronto.edu/~drorbn/KAtlas/Knots/4.1.html.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Broadhurst, D. J. "Massive 3-Loop Feynman Diagrams Reducible to  Primitives of Algebras of the Sixth Root of Unity." March 11, 1998. http://arxiv.org/abs/hep-th/9803091.
Primitives of Algebras of the Sixth Root of Unity." March 11, 1998. http://arxiv.org/abs/hep-th/9803091.
Francis, G. K. A Topological Picture Book. New York: Springer-Verlag, 1987.
Kauffman, L. Knots and Physics. Teaneck, NJ: World Scientific, pp. 8, 12, and 35, 1991.
KnotPlot. " ." http://newweb.cecm.sfu.ca/cgi-bin/KnotPlot/KnotServer/kserver?ncomp=1&ncross=4&id=1.
." http://newweb.cecm.sfu.ca/cgi-bin/KnotPlot/KnotServer/kserver?ncomp=1&ncross=4&id=1.
Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., pp. 21 and 153, 1993.
Owen, P. Knots. Philadelphia, PA: Courage, p. 16, 1993.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 58 and 224, 1976.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. Middlesex, England: Penguin Books, pp. 78-79, 1991.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|