


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-12-2019
Date: 20-10-2020
Date: 23-1-2021
|
Bezdek and Kuperberg (1991) have constructed packings of identical ellipsoids of densities arbitrarily close to
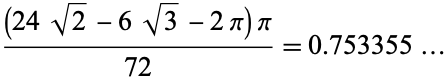 |
(OEIS A093824), greater than the maximum density of 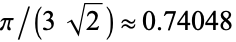 (OEIS A093825) that is possible for sphere packing (Sloane 1998), as established by proof of the Kepler conjecture. Furthermore, J. Wills has modified the ellipsoid packing to yield an even higher density of
(OEIS A093825) that is possible for sphere packing (Sloane 1998), as established by proof of the Kepler conjecture. Furthermore, J. Wills has modified the ellipsoid packing to yield an even higher density of 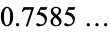 (Bezdek and Kuperberg 1991).
(Bezdek and Kuperberg 1991).
Donev et al. (2004) showed that a maximally random jammed state of M&Ms chocolate candies has a packing density of about 68%, or 4% greater than spheres. Furthermore, Donev et al. (2004) also showed by computer simulations other ellipsoid packings resulted in random packing densities approaching that of the densest sphere packings, i.e., filling nearly 74% of space.
REFERENCES:
Bezdek, A. and Kuperberg, W. In Applied Geometry and Discrete Mathematics: The Victor Klee Festschrift (Ed. P. Gritzmann and B. Sturmfels). Providence, RI: Amer. Math. Soc., pp. 71-80, 1991.
Donev, A.; Cisse, I.; Sachs, D.; Variano, E. A.; Stillinger, F. H.; Connelly, R.; Torquato, S.; and Chaikin, P. M. "Improving the Density of Jammed Disordered Packings using Ellipsoids." Science, 303, 990-993, 2004.
Sloane, N. J. A. "Kepler's Conjecture Confirmed." Nature 395, 435-436, 1998.
Sloane, N. J. A. Sequences A093824 and A093825 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|