


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 31-10-2019
Date: 18-1-2021
Date: 20-9-2020
|
A Trott constant is a real number whose decimal digits are equal to the terms of its continued fraction.
The first Trott constant ![T_1=0.1084101512231113...=[0,1,0,8,4,1,0,1,5,...]](http://mathworld.wolfram.com/images/equations/TrottConstants/Inline1.gif) (OEIS A039662) was discovered by M. Trott in 1999. While it is theoretically possible to extend this sequence arbitrarily far, it is impractical to do so since agreement after 639 terms is so close that the number of consecutive term pairs of "90" that would immediately follow the 639th term would exceed
(OEIS A039662) was discovered by M. Trott in 1999. While it is theoretically possible to extend this sequence arbitrarily far, it is impractical to do so since agreement after 639 terms is so close that the number of consecutive term pairs of "90" that would immediately follow the 639th term would exceed 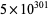 (Schoenfield 2010).
(Schoenfield 2010).
The second Trott constant is the number 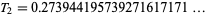 (OEIS A091694; Trott 2004, p. 70) which is equal to its non-simple continued fraction
(OEIS A091694; Trott 2004, p. 70) which is equal to its non-simple continued fraction
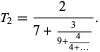 |
The third Trott constant is the number 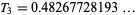 (OEIS A113307; M. Trott, pers. comm., Oct. 24, 2005) which is equal to its non-simple continued fraction
(OEIS A113307; M. Trott, pers. comm., Oct. 24, 2005) which is equal to its non-simple continued fraction
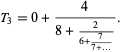 |
Very little seems to be known about the existence and uniqueness of such numbers.
REFERENCES:
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, p. 443, 2003.
Schoenfield, J. "Extending (Arbitrarily Far) the Modified Trott Constant of A114376." Apr. 18, 2010. https://oeis.org/A114376/a114376.txt.
Sloane, N. J. A. Sequences A039662, A091694, and A113307 in "The On-Line Encyclopedia of Integer Sequences."
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.
Trott, M. "Finding Trott Constants." Mathematica J. 10, 303-322, 2006.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|