Let us now go further. Take the example where the temperature of the vanes is T₁ and the temperature of the wheel, or ratchet, is T₂, and T₂ is less than T₁. Because the wheel is cold and the fluctuations of the pawl are relatively infrequent, it will be very hard for the pawl to attain an energy ϵ. Because of the high temperature T₁, the vanes will often attain the energy ϵ, so our gadget will go in one direction, as designed.

We would now like to see if it can lift weights. Onto the drum in the middle, we tie a string, and put a weight, such as our flea, on the string. We let L be the torque due to the weight. If L is not too great, our machine will lift the weight because the Brownian fluctuations make it more likely to move in one direction than the other. We want to find how much weight it can lift, how fast it goes around, and so on.

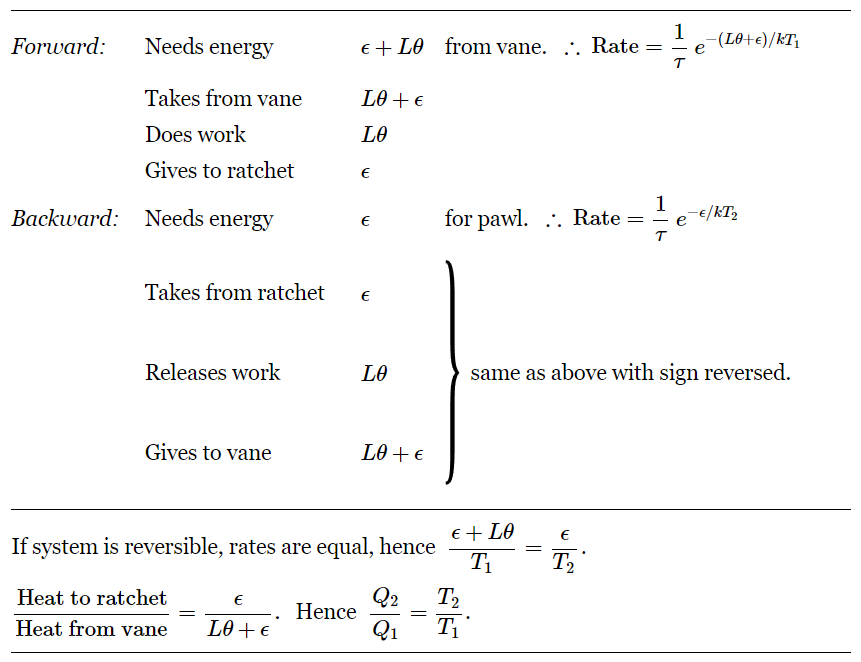
First, we consider a forward motion, the usual way one designs a ratchet to run. In order to make one step forward, how much energy has to be borrowed from the vane end? We must borrow an energy ϵ to lift the pawl. The wheel turns through an angle θ against a torque L, so we also need the energy Lθ. The total amount of energy that we have to borrow is thus ϵ+Lθ. The probability that we get this energy is proportional to e^{−(ϵ+Lθ)/kT1}. Actually, it is not only a question of getting the energy, but we also would like to know the number of times per second it has this energy. The probability per second is proportional to e^{−(ϵ+Lθ)/kT1}, and we shall call the proportionality constant 1/τ. It will cancel out in the end anyway. When a forward step happens, the work done on the weight is Lθ. The energy taken from the vane is ϵ+Lθ. The spring gets wound up with energy ϵ, then it goes clatter, clatter, bang, and this energy goes into heat. All the energy taken out goes to lift the weight and to drive the pawl, which then falls back and gives heat to the other side.

Now we look at the opposite case, which is backward motion. What happens here? To get the wheel to go backwards all we have to do is supply the energy to lift the pawl high enough so that the ratchet will slip. This is still energy ϵ. Our probability per second for the pawl to lift this high is now (1/τ)e^−ϵ/kT2. Our proportionality constant is the same, but this time kT₂ shows up because of the different temperature. When this happens, the work is released because the wheel slips backward. It loses one notch, so it releases work Lθ. The energy taken from the ratchet system is ϵ, and the energy given to the gas at T₁ on the vane side is Lθ+ϵ. It takes a little thinking to see the reason for that. Suppose the pawl has lifted itself up accidentally by a fluctuation. Then when it falls back and the spring pushes it down against the tooth, there is a force trying to turn the wheel, because the tooth is pushing on an inclined plane. This force is doing work, and so is the force due to the weights. So both together make up the total force, and all the energy which is slowly released appears at the vane end as heat. (Of course it must, by conservation of energy, but one must be careful to think the thing through!) We notice that all these energies are exactly the same, but reversed. So, depending upon which of these two rates is greater, the weight is either slowly lifted or slowly released. Of course, it is constantly jiggling around, going up for a while and down for a while, but we are talking about the average behavior.

Suppose that for a particular weight the rates happen to be equal. Then we add an infinitesimal weight to the string. The weight will slowly go down, and work will be done on the machine. Energy will be taken from the wheel and given to the vanes. If instead we take off a little bit of weight, then the imbalance is the other way. The weight is lifted, and heat is taken from the vane and put into the wheel. So we have the conditions of Carnot’s reversible cycle, provided that the weight is just such that these two are equal. This condition is evidently that (ϵ+Lθ)/T₁=ϵ/T₂. Let us say that the machine is slowly lifting the weight. Energy Q₁ is taken from the vanes and energy Q₂ is delivered to the wheel, and these energies are in the ratio (ϵ+Lθ)/ϵ. If we are lowering the weight, we also have Q₁/Q₂=(ϵ+Lθ)/ϵ. Thus (Table 46–1) we have

Q₁/Q₂ = T₁/T₂.

Furthermore, the work we get out is to the energy taken from the vane as Lθ is to Lθ+ϵ, hence as (T₁−T₂)/T₁. We see that our device cannot extract more work than this, operating reversibly. This is the result that we expected from Carnot’s argument, and the main result of this lecture. However, we can use our device to understand a few other phenomena, even out of equilibrium, and therefore beyond the range of thermodynamics.

Table 46–1

Summary of operation of ratchet and pawl.

Let us now calculate how fast our one-way device would turn if everything were at the same temperature and we hung a weight on the drum. If we pull very, very hard, of course, there are all kinds of complications. The pawl slips over the ratchet, or the spring breaks, or something. But suppose we pull gently enough that everything works nicely. In those circumstances, the above analysis is right for the probability of the wheel going forward and backward, if we remember that the two temperatures are equal. In each step an angle θ is obtained, so the angular velocity is θ times the probability of one of these jumps per second. It goes forward with probability (1/τ)e^{−(ϵ+Lθ)/kT} and backward with probability (1/τ)e^−ϵ/kT, so that for the angular velocity we have

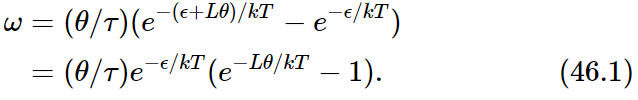
If we plot ω against L, we get the curve shown in Fig. 46–2. We see that it makes a great difference whether L is positive or negative. If L increases in the positive range, which happens when we try to drive the wheel backward, the backward velocity approaches a constant. As L becomes negative, ω really “takes off” forward, since e to a tremendous power is very great!

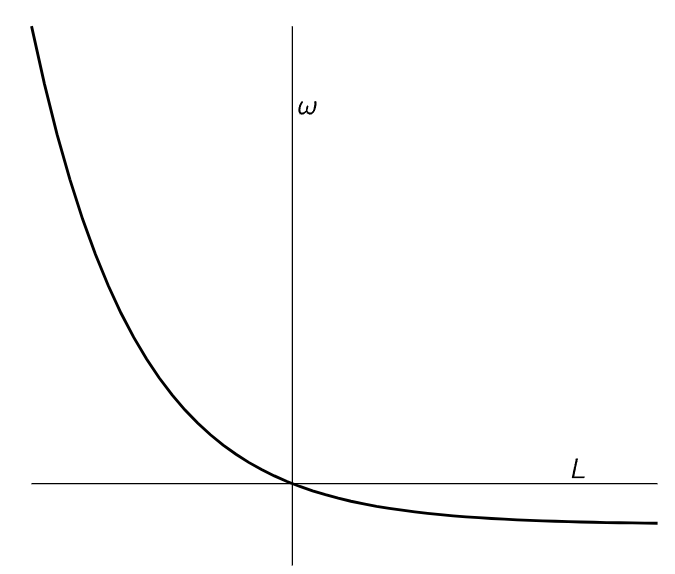
Fig. 46–2. Angular velocity of the ratchet as a function of torque.

The angular velocity that was obtained from different forces is thus very unsymmetrical. Going one way it is easy: we get a lot of angular velocity for a little force. Going the other way, we can put on a lot of force, and yet the wheel hardly goes around.

We find the same thing in an electrical rectifier. Instead of the force, we have the electric field, and instead of the angular velocity, we have the electric current. In the case of a rectifier, the voltage is not proportional to resistance, and the situation is unsymmetrical. The same analysis that we made for the mechanical rectifier will also work for an electrical rectifier. In fact, the kind of formula we obtained above is typical of the current-carrying capacities of rectifiers as a function of their voltages.

Now let us take all the weights away, and look at the original machine. If T₂ were less than T₁, the ratchet would go forward, as anybody would believe. But what is hard to believe, at first sight, is the opposite. If T₂ is greater than T₁, the ratchet goes around the opposite way! A dynamic ratchet with lots of heat in it runs itself backwards, because the ratchet pawl is bouncing. If the pawl, for a moment, is on the incline somewhere, it pushes the inclined plane sideways. But it is always pushing on an inclined plane, because if it happens to lift up high enough to get past the point of a tooth, then the inclined plane slides by, and it comes down again on an inclined plane. So a hot ratchet and pawl is ideally built to go around in a direction exactly opposite to that for which it was originally designed!

In spite of all our cleverness of lopsided design, if the two temperatures are exactly equal there is no more propensity to turn one way than the other. The moment we look at it, it may be turning one way or the other, but in the long run, it gets nowhere. The fact that it gets nowhere is really the fundamental deep principle on which all of thermodynamics is based.