


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-5-2020
Date: 8-1-2020
Date: 10-10-2020
|
A linear congruence equation
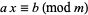 |
(1) |
is solvable iff the congruence
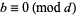 |
(2) |
with 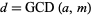 is the greatest common divisor is solvable. Let one solution to the original equation be
is the greatest common divisor is solvable. Let one solution to the original equation be 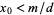 . Then the solutions are
. Then the solutions are 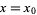 ,
, 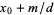 ,
, 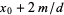 , ...,
, ..., 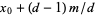 . If
. If 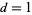 , then there is only one solution
, then there is only one solution 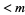 .
.
The solution of a linear congruence can be found in the Wolfram Language using Reduce[a*x == b, x, Modulus -> m].
Solution to a linear congruence equation is equivalent to finding the value of a fractional congruence, for which a greedy-type algorithm exists. In particular, (1) can be rewritten as
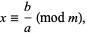 |
(3) |
which can also be written
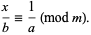 |
(4) |
In this form, the solution  can be found as Mod[b y, m] of the solution
can be found as Mod[b y, m] of the solution 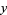 returned by the Wolfram Language function PowerMod[a,
returned by the Wolfram Language function PowerMod[a, 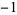 , m]. This is known as a modular inverse.
, m]. This is known as a modular inverse.
Two or more simultaneous linear congruences
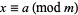 |
(5) |
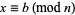 |
(6) |
are solvable using the Chinese remainder theorem.
REFERENCES:
Nagell, T. "Linear Congruences." §23 in Introduction to Number Theory. New York: Wiley, pp. 76-78, 1951.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
المجمع العلمي يقيم ورشة تطويرية ودورة قرآنية في النجف والديوانية
|
|
|