Let there be 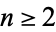 integers  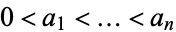with 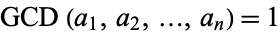. The values  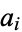represent the denominations of  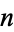different coins, where these denominations have greatest common divisor of 1. The sums of money that can be represented using the given coins are then given by

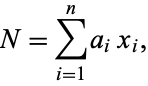(1)

where the 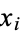 are nonnegative integers giving the numbers of each coin used. If 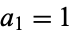, it is obviously possibly to represent any quantity of money 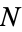. However, in the general case, only some quantities  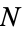can be produced. For example, if the allowed coins are 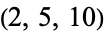, it is impossible to represent  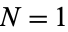and 3, although all other quantities can be represented.

Determining the function 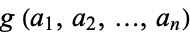 giving the greatest  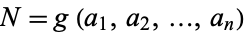for which there is no solution is called the coin problem, or sometimes the money-changing problem. The largest such  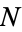for a given problem is called the Frobenius number .

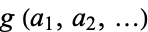The result

			(2)
			(3)

(Nijenhuis and Wilf 1972) is mathematical folklore. The total number of such nonrepresentable amounts is given by

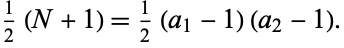(4)

The largest nonrepresentable amounts 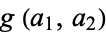 for two coins with denominations  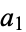and 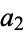 are summarized below.

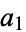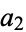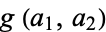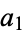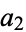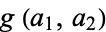2	3	1	4	7	17
2	5	3	4	9	23
2	7	5	5	6	19
2	9	7	5	7	23
3	4	5	5	8	27
3	5	7	5	9	31
3	7	11	6	7	29
3	8	13	7	8	41
3	10	17	7	9	47
4	5	11	7	10	53

Fast algorithms are also known for three numbers, but the more general problem for an arbitrary number of numbers is known to be NP-hard if 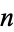 is fixed (Kannan 1992) or  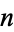is variable (Ramírez-Alfonsín 1996).

There is no closed-form solution for 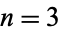, although a semi-explicit solution is known which allows values to be computed quickly ((Selmer and Beyer 1978, Rödseth 1978, Greenberg 1988; Beck and Robins 2006). Values for small  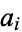are summarized below.

	1		5
	1		3
	1		3
	1		5
	3		2

No closed-form solution is known for .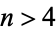

REFERENCES:

Beck, M. and Robins, S. "The Coin-Exchange Problem of Frobenius." §C1 in Computing the Continuous Discretely. New York: Springer, pp. 3-23, 2006. https://math.sfsu.edu/beck/ccd.html.

Berlekamp, E. R.; Conway, J. H; and Guy, R. K. Winning Ways for Your Mathematical Plays, Vol. 2: Games in Particular. London: Academic Press, 1982.

Brauer, A. "On a Problem of Partitions." Amer. J. Math. 64, 299-312, 1942.

Brauer, A. and Seelbinder, B. M. "On a Problem of Partitions. II." Amer. J. Math. 76, 343-346, 1954.

Davison, J. L. "On the Linear Diophantine Problem of Frobenius." J. Number Th. 48, 353-363, 1994.

Greenberg, H. "Solution to a Linear Diophantine Equation for Nonnegative Integers." J. Algorithms 9, 343-353, 1988.

Guy, R. K. "The Money-Changing Problem." §C7 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 113-114, 1994.

Kannan, R. "Lattice Translates of a Polytope and the Frobenius Problem." Combinatorica 12, 161-177, 1992.

Nabiyev, V. V. Algorithms: From Theory to Applications. Ankara, Turkey: Seckin, p. 799, 2007.

Nijenhuis, A. "A Minimal-Path Algorithm for the 'Money Changing Problem.' " Amer. Math. Monthly 86, 832-835, 1979.

Nijenhuis, A. and Wilf, H. S. "Representations of Integers by Linear Forms in Nonnegative Integers." J. Number Th. 4, 98-106, 1972.

Ramírez-Alfonsín, J. L. "Complexity of the Frobenius Problem." Combinatorica 16, 143-147, 1996.

Ramírez-Alfonsín, J. L. The Diophantine Frobenius Problem. Oxford, England: Oxford University Press, 2005.

Rødseth, Ø. J. "On a Linear Diophantine Problem of Frobenius." J. reine angew. Math. 301, 171-178, 1978.

Rødseth, Ø. J. "On a Linear Diophantine Problem of Frobenius. II." J. reine angew. Math. 307/308, 431-440, 1979.

Selmer, E. S. "The Linear Diophantine Problem of Frobenius." J. reine angew. Math. 293/294, 1-17, 1977.

Selmer, E. S. and Beyer, Ö. "On the Linear Diophantine Problem of Frobenius in Three Variables." J. reine angew. Math. 301, 161-170, 1978.

Sylvester, J. J. "Question 7382." Mathematical Questions from the Educational Times 41, 21, 1884.

 Wagon, S. "Greedy Coins." https://library.wolfram.com/infocenter/MathSource/5187/.

Wilf, H. "A Circle of Lights Algorithm for the 'Money Changing Problem.' " Amer. Math. Monthly 85, 562-565, 1978.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الفكرية يطلق باقة من النشاطات الرقمية الخاصة بشهر المحرم

العتبة العباسية المقدسة تختتم السلسلة الأولى لمشروع المحاضرات القرآنية العاشورائية في بابل

العتبة العباسية المقدسة تسلّم راية العزاء إلى تجمّع مواكب محافظة الديوانية

قسم الشؤون الفكرية يواصل إقامة المجالس الحسينية ضمن سلسلة (بيوت النعيم)

المزيد

الآخبار الصحية

تناول الجبن.. مفيد للجسم أم خطر يهدد صحتك؟

طبيبة أسنان تحذر.. لا تتجاهل هذه العلامة بعد التنظيف

يجب أن تأكل المزيد من الشمام هذا الصيف.. إليك السبب ؟

تأثير صحي كبير.. كم بيضة يجب أن تتناول يوميا؟

المزيد

الآخبار التكنلوجية

أداء خلايا البيروفسكايت الشمسية تحت الماء قد يزيد كفاءة تحويل الكهرباء

مسافة الأمان: أساس القيادة الآمنة وتجنب الحوادث

هل القيادة السريعة تعني استهلاك اكثر للوقود؟

لماذا يعتبر كوكب المريخ غير صالح للحياة؟

المزيد