Artin's Conjecture

There are at least two statements which go by the name of Artin's conjecture.

If 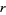 is any complex finite-dimensional representation of the absolute Galois group of a number field, then Artin showed how to associate an 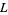-series  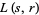with it. These 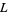-series directly generalize zeta functions and Dirichlet 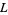-series, and as a result of work by Richard Brauer,  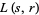is known to extend to a meromorphic function on the complex plane. Artin's conjecture predicts that it is in fact holomorphic, i.e., has no poles, with the possible exception of a pole at  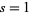(Artin 1923/1924). Compare with the generalized Riemann hypothesis, which deals with the locations of the zeros of certain 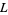-series.

The second conjecture states that every integer not equal to 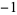 or a square number is a primitive root modulo  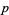for infinitely many  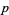and proposes a density for the set of such  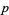which are always rational multiples of a constant known as Artin's constant. There is an analogous theorem for functions instead of numbers which has been proved by Billharz (Shanks 1993, p. 147).

REFERENCES:

Artin, E. "Über eine neue Art von 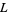-Reihen." Abh. Math. Sem. Univ. Hamburg 3, 89-108, 1923/1924.

Matthews, K. R. "A Generalization of Artin's Conjecture for Primitive Roots." Acta Arith. 29, 113-146, 1976.

Moree, P. "A Note on Artin's Conjecture." Simon Stevin 67, 255-257, 1993.

Ram Murty, M. "Artin's Conjecture for Primitive Roots." Math. Intell. 10, 59-67, 1988.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 31, 80-83, and 147, 1993.