


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-2-2020
Date: 1-11-2020
Date: 12-8-2020
|
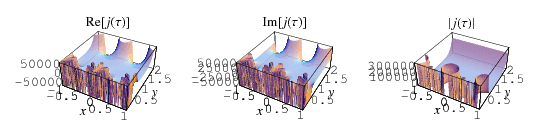

The 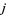 -function is the modular function defined by
-function is the modular function defined by
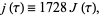 |
(1) |
where  is the half-period ratio,
is the half-period ratio, ![I[tau]>0](http://mathworld.wolfram.com/images/equations/j-Function/Inline3.gif) ,
,
![J(tau)=4/(27)([1-lambda(tau)+lambda^2(tau)]^3)/(lambda^2(tau)[1-lambda(tau)]^2)](http://mathworld.wolfram.com/images/equations/j-Function/NumberedEquation2.gif) |
(2) |
is Klein's absolute invariant, 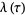 is the elliptic lambda function
is the elliptic lambda function
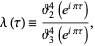 |
(3) |
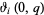 are Jacobi theta functions,
are Jacobi theta functions,
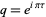 |
(4) |
is the nome, and 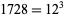 .
.
Gauss was apparently aware of the 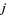 -function before 1800. Hermite used it in solving the quintic in about 1858. Dedekind gave a nice definition in about 1877, and Klein studied the function beginning in 1879 or 1880. The
-function before 1800. Hermite used it in solving the quintic in about 1858. Dedekind gave a nice definition in about 1877, and Klein studied the function beginning in 1879 or 1880. The 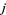 -function is related to the factors of the group order of the monster group and to supersingular primes (Ogg 1980).
-function is related to the factors of the group order of the monster group and to supersingular primes (Ogg 1980).
This function can also be specified in terms of the Weber functions 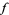 ,
, 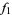 ,
, 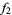 ,
, 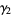 , and
, and 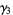 as
as
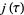 |
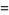 |
![([f^(24)(tau)-16]^3)/(f^(24)(tau))](http://mathworld.wolfram.com/images/equations/j-Function/Inline16.gif) |
(5) |
 |
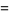 |
![([f_1^(24)(tau)+16]^3)/(f_1^(24)(tau))](http://mathworld.wolfram.com/images/equations/j-Function/Inline19.gif) |
(6) |
 |
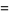 |
![([f_2^(24)(tau)+16]^3)/(f_2^(24)(tau))](http://mathworld.wolfram.com/images/equations/j-Function/Inline22.gif) |
(7) |
 |
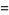 |
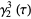 |
(8) |
 |
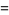 |
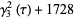 |
(9) |
(Weber 1979, p. 179; Atkin and Morain 1993).
The 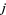 -function is an analytic function on the upper half-plane which is invariant with respect to the special linear group
-function is an analytic function on the upper half-plane which is invariant with respect to the special linear group 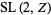 . It has a Fourier series
. It has a Fourier series
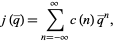 |
(10) |
where
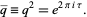 |
(11) |
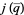 is therefore related
is therefore related 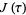 via
via
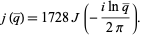 |
(12) |
The coefficients in the expansion of the 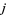 -function satisfy:
-function satisfy:
1.  for
for 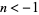 and
and 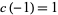 ,
,
2. all 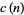 s are integers with fairly limited growth with respect to
s are integers with fairly limited growth with respect to 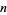 , and
, and
3. 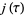 is an algebraic number, sometimes a rational number, and sometimes even an integer at certain very special values of
is an algebraic number, sometimes a rational number, and sometimes even an integer at certain very special values of  .
.
The latter result is the end result of the massive and beautiful theory of complex multiplication and the first step of Kronecker's so-called "Jugendtraum."
Therefore all of the coefficients in the Laurent series
 |
(13) |
(OEIS A000521) are positive integers (Rankin 1977, Apostol 1997). Berwick (1916) calculated the first seven  , Zuckerman (1939) found the first 24, and van Wijngaarden (193) gave the first 100.
, Zuckerman (1939) found the first 24, and van Wijngaarden (193) gave the first 100.
Some remarkable sum formulas involving  for
for 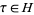 , where
, where 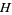 is the upper half-plane, and
is the upper half-plane, and 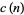 include
include
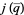 |
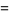 |
![([1+240sum_(n=1)^(infty)sigma_3(n)q^_^n]^3)/(q^_product_(n=1)^(infty)(1-q^_^n)^(24))](http://mathworld.wolfram.com/images/equations/j-Function/Inline48.gif) |
(14) |
 |
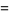 |
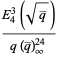 |
(15) |
 |
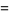 |
![([theta_2^8(sqrt(q^_))+theta_3^8(sqrt(q^_))+theta_2^4(sqrt(q^_))]^3)/(8q^_(q^_)_infty^(24)),](http://mathworld.wolfram.com/images/equations/j-Function/Inline54.gif) |
(16) |
where 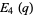 is an Eisenstein series,
is an Eisenstein series, 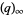 is a q-Pochhammer symbol, and
is a q-Pochhammer symbol, and
![[-1+504sum_(n=1)^inftysigma_5(n)q^_^n]^2=[j(q^_)-12^3]sum_(n=1)^inftytau(n)q^_^n,](http://mathworld.wolfram.com/images/equations/j-Function/NumberedEquation9.gif) |
(17) |
where 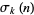 is the divisor function, and
is the divisor function, and 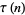 is the tau function (not to be confused with the half-period ratio
is the tau function (not to be confused with the half-period ratio  ). In addition,
). In addition,
![504^2[-2/(504)sigma_5(n)+sum_(k=1)^(n-1)sigma_5(k)sigma_5(n-k)]
=tau(n+1)-984tau(n)+sum_(k=1)^(n-1)c(k)tau(n-k)
(65520)/(691)[sigma_(11)(n)-tau(n)]
=tau(n+1)+24tau(n)+sum_(k=1)^(n-1)c(k)tau(n-k)](http://mathworld.wolfram.com/images/equations/j-Function/NumberedEquation10.gif) |
(18) |
(Lehmer 1942; Apostol 1997, p. 92). These are closely related to Eisenstein series.
Equation (18) leads immediately to the remarkable congruence
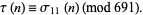 |
(19) |
Lehmer (1942) showed that
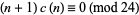 |
(20) |
for all 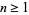 , and Lehner (1949ab) and Apostol (1997, pp. 22, 74, and 90-91) demonstrated that
, and Lehner (1949ab) and Apostol (1997, pp. 22, 74, and 90-91) demonstrated that
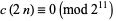 |
(21) |
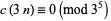 |
(22) |
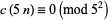 |
(23) |
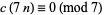 |
(24) |
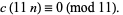 |
(25) |
More generally,
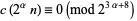 |
(26) |
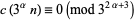 |
(27) |
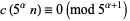 |
(28) |
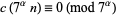 |
(29) |
(Lehner 1949ab; Apostol 1997, p. 91). Congruences of this type cannot exist for 13, but Newman (1958) showed
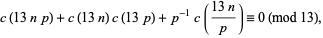 |
(30) |
where 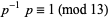 and
and 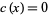 if
if  is not an integer (Apostol 1997, p. 91). Congruences for
is not an integer (Apostol 1997, p. 91). Congruences for 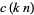 have been generalized by Atkin and O'Brien (1967).
have been generalized by Atkin and O'Brien (1967).
An asymptotic formula for 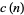 was discovered by Petersson (1932), and subsequently independently rediscovered by Rademacher (1938):
was discovered by Petersson (1932), and subsequently independently rediscovered by Rademacher (1938):
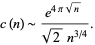 |
(31) |
Let 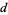 be a squarefree positive integer, and define the half-period ratio by
be a squarefree positive integer, and define the half-period ratio by
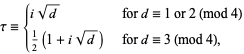 |
(32) |
so
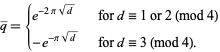 |
(33) |
It then turns out that 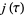 is an algebraic integer of degree
is an algebraic integer of degree 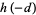 , where
, where 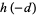 is the class number of the binary quadratic form discriminant
is the class number of the binary quadratic form discriminant 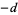 of the quadratic field
of the quadratic field 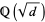 (Silverman 1986; Berndt 1994, p. 90).
(Silverman 1986; Berndt 1994, p. 90).
If 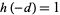 , then
, then 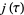 is an algebraic integer of degree 1, i.e., just a plain integer. Furthermore, the integer is a perfect cube. But these are precisely the Heegner numbers
is an algebraic integer of degree 1, i.e., just a plain integer. Furthermore, the integer is a perfect cube. But these are precisely the Heegner numbers 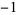 ,
, 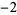 ,
, 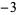 ,
, 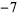 ,
, 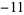 ,
, 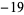 ,
, 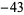 ,
, 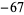 ,
, 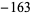 . The exact values of
. The exact values of 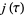 corresponding to the Heegner numbers are
corresponding to the Heegner numbers are
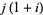 |
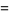 |
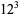 |
(34) |
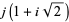 |
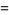 |
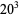 |
(35) |
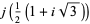 |
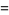 |
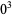 |
(36) |
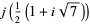 |
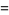 |
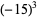 |
(37) |
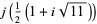 |
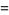 |
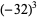 |
(38) |
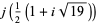 |
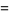 |
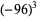 |
(39) |
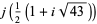 |
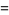 |
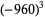 |
(40) |
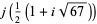 |
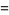 |
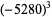 |
(41) |
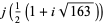 |
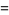 |
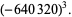 |
(42) |
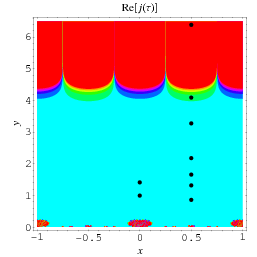
The positions of these special values of  are illustrated above. (Note the curious though not particularly significant fact that number 5280 is also the number of feet in a mile.)
are illustrated above. (Note the curious though not particularly significant fact that number 5280 is also the number of feet in a mile.)
The greater (in absolute value) the Heegner number 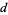 , the closer to an integer is the expression
, the closer to an integer is the expression 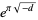 , since the initial term in
, since the initial term in 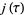 is the largest and subsequent terms are the smallest. The best approximations with
is the largest and subsequent terms are the smallest. The best approximations with 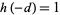 are therefore
are therefore
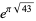 |
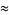 |
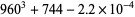 |
(43) |
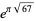 |
 |
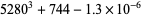 |
(44) |
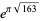 |
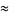 |
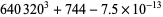 |
(45) |
(the latter of which appears in Trott 2004, p. 8). The almost integer generated by the last of these, 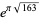 (corresponding to the field
(corresponding to the field 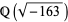 and the imaginary quadratic field of maximal discriminant), is sometimes known as the Ramanujan constant. However, this attribution is historically fallacious since this amazing property of
and the imaginary quadratic field of maximal discriminant), is sometimes known as the Ramanujan constant. However, this attribution is historically fallacious since this amazing property of 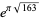 was first noted by Hermite (1859) and does not seem to appear in any of the works of Ramanujan.
was first noted by Hermite (1859) and does not seem to appear in any of the works of Ramanujan.
There are 18 numbers having class number 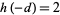 , with the odd discriminants not divisible by three corresponding to the exact values
, with the odd discriminants not divisible by three corresponding to the exact values
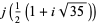 |
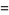 |
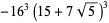 |
(46) |
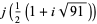 |
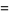 |
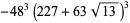 |
(47) |
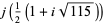 |
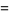 |
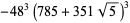 |
(48) |
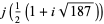 |
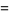 |
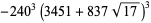 |
(49) |
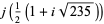 |
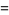 |
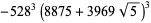 |
(50) |
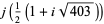 |
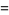 |
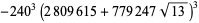 |
(51) |
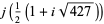 |
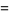 |
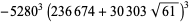 |
(52) |
and even 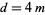 for
for 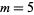 , 10, 13, 22, 37, 58,
, 10, 13, 22, 37, 58,
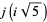 |
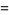 |
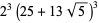 |
(53) |
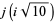 |
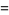 |
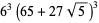 |
(54) |
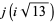 |
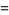 |
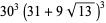 |
(55) |
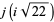 |
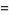 |
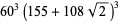 |
(56) |
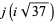 |
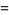 |
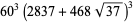 |
(57) |
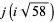 |
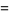 |
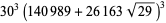 |
(58) |
and discriminants divisible by 3,
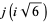 |
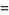 |
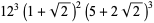 |
(59) |
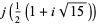 |
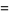 |
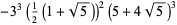 |
(60) |
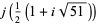 |
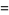 |
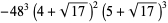 |
(61) |
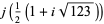 |
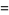 |
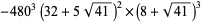 |
(62) |
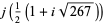 |
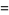 |
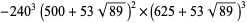 |
(63) |
with the square factor being a fundamental unit.
The best approximations for 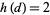 are, for even discriminants,
are, for even discriminants,
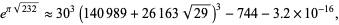 |
(64) |
and for odd discriminants,
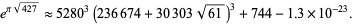 |
(65) |
The numbers
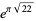 |
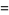 |
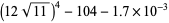 |
(66) |
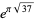 |
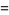 |
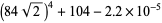 |
(67) |
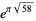 |
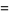 |
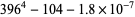 |
(68) |
are also almost integers. These correspond to binary quadratic forms with discriminants 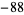 ,
, 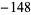 , and
, and 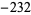 , which are the largest (in absolute value) discriminants with class number two that are divisible by 4. They were noted by Ramanujan (Berndt 1994, pp. 88-91).
, which are the largest (in absolute value) discriminants with class number two that are divisible by 4. They were noted by Ramanujan (Berndt 1994, pp. 88-91).
REFERENCES:
Apostol, T. M. "The Fourier Expansions of 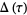 and
and 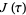 " and "Congruences for the Coefficients of the Modular Function
" and "Congruences for the Coefficients of the Modular Function 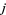 ." §1.15 and Ch. 4 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 20-22 and 74-93, 1997.
." §1.15 and Ch. 4 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 20-22 and 74-93, 1997.
Atkin, A. O. L. and Morain, F. "Elliptic Curves and Primality Proving." Math. Comput. 61, 29-68, 1993.
Atkin, A. O. L. and O'Brien, J. N. "Some Properties of 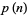 and
and 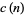 Modulo Powers of 13." Trans. Amer. Math. Soc. 126, 442-459, 1967.
Modulo Powers of 13." Trans. Amer. Math. Soc. 126, 442-459, 1967.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Berwick, W. E. H. "An Invariant Modular Equation of the Fifth Order." Quart. J. Math. 47, 94-103, 1916.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 117-118, 1987.
Cohen, H. In From Number Theory to Physics (M. Waldschmidt, P. Moussa, J.-M. Luck, and C. Itzykson). Berlin: Springer-Verlag, 1992.
Cohn, H. Introduction to the Construction of Class Fields. New York: Dover, p. 73, 1994.
Conway, J. H. and Guy, R. K. "The Nine Magic Discriminants." In The Book of Numbers. New York: Springer-Verlag, pp. 224-226, 1996.
Hermite, C. "Sur la théorie des équations modulaires." Comptes Rendus Acad. Sci. Paris 49, 16-24, 110-118, and 141-144, 1859 Oeuvres complètes, Tome II. Paris: Hermann, p. 61, 1912.
Lehmer, D. H. "Properties of the Coefficients of the Modular Invariant 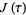 ." Amer. J. Math. 64, 488-502, 1942.
." Amer. J. Math. 64, 488-502, 1942.
Lehner, J. "Divisibility Properties of the Fourier Coefficients of the Modular Invariant 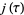 ." Amer. J. Math. 71, 136-148, 1949a.
." Amer. J. Math. 71, 136-148, 1949a.
Lehner, J. "Further Congruence Properties of the Fourier Coefficients of the Modular Invariant 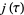 ." Amer. J. Math. 71, 373-386, 1949b.
." Amer. J. Math. 71, 373-386, 1949b.
Morain, F. "Implementation of the Atkin-Goldwasser-Kilian Primality Testing Algorithm." Rapport de Recherche 911, INRIA, Oct. 1988.
Newman, M. "Congruences for the Coefficients of Modular Forms and for the Coefficients of 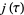 ." Proc. Amer. Math. Soc. 9, 609-612, 1958.
." Proc. Amer. Math. Soc. 9, 609-612, 1958.
Ogg, A. P. "Modular Functions." In The Santa Cruz Conference on Finite Groups. Held at the University of California, Santa Cruz, Calif., June 25-July 20, 1979 (Ed. B. Cooperstein and G. Mason). Providence, RI: Amer. Math. Soc., pp. 521-532, 1980.
Petersson, H. "Über die Entwicklungskoeffizienten der automorphen formen." Acta Math. 58, 169-215, 1932.
Piezas, T. "Ramanujan's Constant and Its Cousins." 2005. http://www.geocities.com/titus_piezas/Ramanujan_a.htm.
Rademacher, H. "The Fourier Coefficients of the Modular Invariant 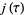 ." Amer. J. Math. 60, 501-512, 1938.
." Amer. J. Math. 60, 501-512, 1938.
Rankin, R. A. Modular Forms and Functions. Cambridge, England: Cambridge University Press, p. 199, 1977.
Rankin, R. A. Modular Forms. New York: Wiley, 1985.
Roberts, J. The Lure of the Integers. Washington, DC: Math. Assoc. Amer., 1992.
Serre, J.-P. A Course in Arithmetic. New York: Springer-Verlag, 1973.
Silverman, J. H. The Arithmetic of Elliptic Curves. New York: Springer-Verlag, p. 339, 1986.
Sloane, N. J. A. Sequence A000521/M5477 in "The On-Line Encyclopedia of Integer Sequences."
Stillwell, J. "Modular Miracles." Amer. Math. Monthly 108, 70-76, 2001.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.
van Wijngaarden, A. "On the Coefficients of the Modular Invariant 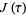 ." Indagationes Math. 15, 389-400, 1953.
." Indagationes Math. 15, 389-400, 1953.
Waldschmidt, M. In Ramanujan Centennial International Conference (Ed. R. Balakrishnan, K. S. Padmanabhan, and V. Thangaraj). Ramanujan Math. Soc., 1988.
Weber, H. Lehrbuch der Algebra, Vols. I-II. New York: Chelsea, 1979.
Zuckerman, H. S. "The Computation of the Smaller Coefficients of 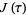 ." Bull. Amer. Math. Soc. 45, 917-919, 1939.
." Bull. Amer. Math. Soc. 45, 917-919, 1939.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|