


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-12-2020
Date: 12-7-2020
Date: 24-10-2020
|
Let 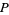 ,
, 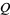 be integers satisfying
be integers satisfying
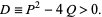 |
(1) |
Then roots of
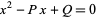 |
(2) |
are
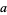 |
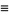 |
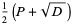 |
(3) |
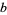 |
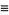 |
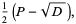 |
(4) |
so
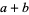 |
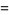 |
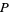 |
(5) |
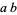 |
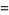 |
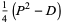 |
(6) |
 |
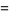 |
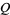 |
(7) |
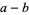 |
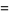 |
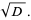 |
(8) |
Now define
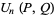 |
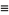 |
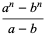 |
(9) |
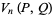 |
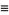 |
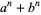 |
(10) |
for integer 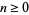 , so the first few values are
, so the first few values are
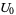 |
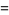 |
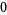 |
(11) |
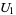 |
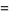 |
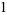 |
(12) |
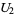 |
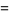 |
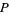 |
(13) |
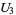 |
 |
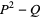 |
(14) |
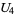 |
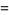 |
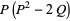 |
(15) |
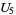 |
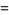 |
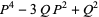 |
(16) |
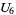 |
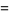 |
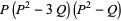 |
(17) |
 |
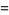 |
 |
(18) |
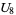 |
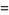 |
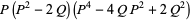 |
(19) |
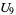 |
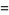 |
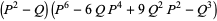 |
(20) |
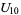 |
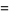 |
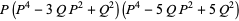 |
(21) |
and
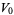 |
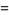 |
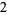 |
(22) |
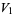 |
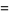 |
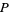 |
(23) |
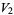 |
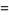 |
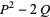 |
(24) |
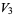 |
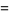 |
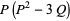 |
(25) |
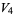 |
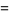 |
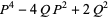 |
(26) |
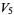 |
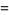 |
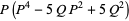 |
(27) |
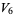 |
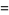 |
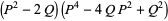 |
(28) |
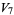 |
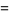 |
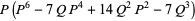 |
(29) |
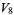 |
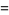 |
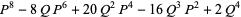 |
(30) |
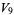 |
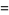 |
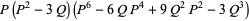 |
(31) |
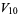 |
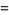 |
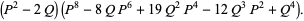 |
(32) |
Closed forms for these are given by
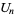 |
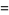 |
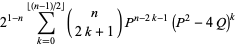 |
(33) |
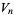 |
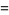 |
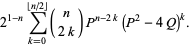 |
(34) |
The sequences
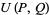 |
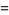 |
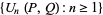 |
(35) |
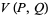 |
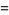 |
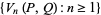 |
(36) |
are called Lucas sequences, where the definition is usually extended to include
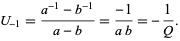 |
(37) |
The following table summarizes special cases of 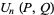 and
and 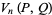 .
.
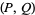 |
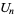 |
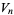 |
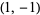 |
Fibonacci numbers | Lucas numbers |
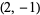 |
Pell numbers | Pell-Lucas numbers |
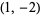 |
Jacobsthal numbers | Pell-Jacobsthal numbers |
The Lucas sequences satisfy the general recurrence relations
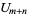 |
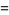 |
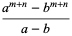 |
(38) |
 |
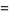 |
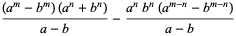 |
(39) |
 |
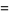 |
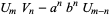 |
(40) |
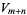 |
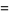 |
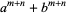 |
(41) |
 |
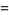 |
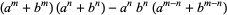 |
(42) |
 |
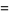 |
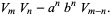 |
(43) |
Taking  then gives
then gives
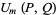 |
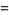 |
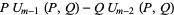 |
(44) |
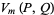 |
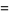 |
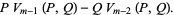 |
(45) |
Other identities include
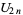 |
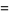 |
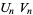 |
(46) |
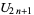 |
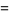 |
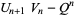 |
(47) |
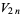 |
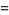 |
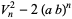 |
(48) |
 |
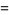 |
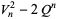 |
(49) |
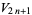 |
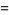 |
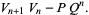 |
(50) |
These formulas allow calculations for large 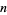 to be decomposed into a chain in which only four quantities must be kept track of at a time, and the number of steps needed is
to be decomposed into a chain in which only four quantities must be kept track of at a time, and the number of steps needed is 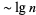 . The chain is particularly simple if
. The chain is particularly simple if 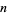 has many 2s in its factorization.
has many 2s in its factorization.
REFERENCES:
Dickson, L. E. "Recurring Series; Lucas' 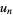 ,
, 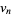 ." Ch. 17 in History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 393-411, 2005.
." Ch. 17 in History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 393-411, 2005.
Ribenboim, P. The Little Book of Big Primes. New York: Springer-Verlag, pp. 35-53, 1991.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|