


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-6-2019
Date: 20-7-2019
Date: 15-6-2019
|
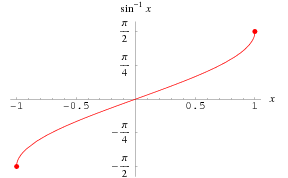
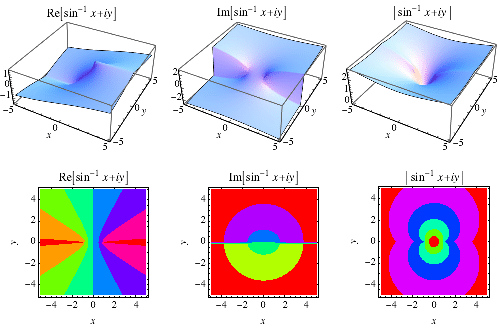 |
The inverse sine is the multivalued function 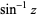 (Zwillinger 1995, p. 465), also denoted
(Zwillinger 1995, p. 465), also denoted 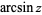 (Abramowitz and Stegun 1972, p. 79; Harris and Stocker 1998, p. 307; Jeffrey 2000, p. 124), that is the inverse function of the sine. The variants
(Abramowitz and Stegun 1972, p. 79; Harris and Stocker 1998, p. 307; Jeffrey 2000, p. 124), that is the inverse function of the sine. The variants 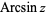 (e.g., Bronshtein and Semendyayev, 1997, p. 69) and
(e.g., Bronshtein and Semendyayev, 1997, p. 69) and 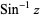 are sometimes used to refer to explicit principal values of the inverse sine, although this distinction is not always made (e.g,. Zwillinger 1995, p. 466). Worse yet, the notation
are sometimes used to refer to explicit principal values of the inverse sine, although this distinction is not always made (e.g,. Zwillinger 1995, p. 466). Worse yet, the notation 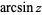 is sometimes used for the principal value, with
is sometimes used for the principal value, with 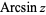 being used for the multivalued function (Abramowitz and Stegun 1972, p. 80). Note that in the notation
being used for the multivalued function (Abramowitz and Stegun 1972, p. 80). Note that in the notation 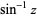 (commonly used in North America and in pocket calculators worldwide),
(commonly used in North America and in pocket calculators worldwide), 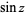 is the sine and the superscript
is the sine and the superscript 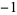 denotes the inverse function, not the multiplicative inverse.
denotes the inverse function, not the multiplicative inverse.
The principal value of the inverse sine is implemented as ArcSin[z] in the Wolfram Language. In the GNU C library, it is implemented as asin(double x).
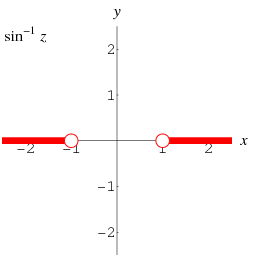
The inverse sine is a multivalued function and hence requires a branch cut in the complex plane, which the Wolfram Language's convention places at 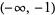 and
and 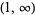 . This follows from the definition of
. This follows from the definition of 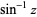 as
as
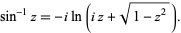 |
(1) |
Special values include
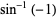 |
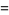 |
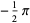 |
(2) |
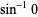 |
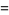 |
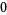 |
(3) |
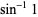 |
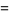 |
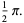 |
(4) |
The derivative of 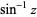 is
is
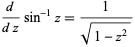 |
(5) |
and its indefinite integral is
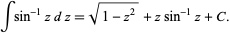 |
(6) |
The inverse sine satisfies
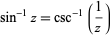 |
(7) |
for 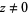 ,
,
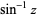 |
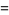 |
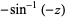 |
(8) |
 |
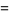 |
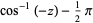 |
(9) |
 |
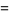 |
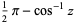 |
(10) |
for all complex 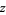 ,
,
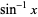 |
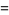 |
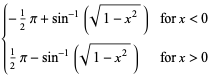 |
(11) |
 |
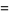 |
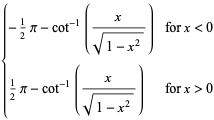 |
(12) |
 |
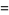 |
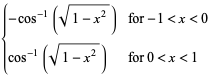 |
(13) |
 |
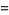 |
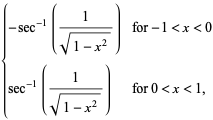 |
(14) |
and
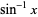 |
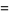 |
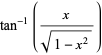 |
(15) |
 |
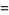 |
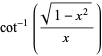 |
(16) |
for 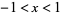 , where equality at points where the denominators are 0 is understood to mean in the limit as
, where equality at points where the denominators are 0 is understood to mean in the limit as 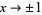 or
or 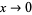 , respectively.
, respectively.
The Maclaurin series for the inverse sine with 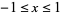 is given by
is given by
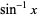 |
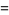 |
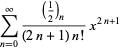 |
(17) |
 |
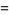 |
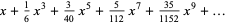 |
(18) |
(OEIS A055786 and A002595), where 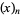 is a Pochhammer symbol.
is a Pochhammer symbol.
The inverse sine can be given by the sum
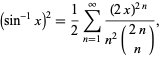 |
(19) |
where 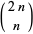 is a binomial coefficient (Borwein et al. 2004, p. 51; Borwein and Chamberland 2005; Bailey et al. 2007, pp. 15-16). Similarly,
is a binomial coefficient (Borwein et al. 2004, p. 51; Borwein and Chamberland 2005; Bailey et al. 2007, pp. 15-16). Similarly,
![[sin^(-1)(1/2x)]^4](http://mathworld.wolfram.com/images/equations/InverseSine/Inline64.gif) |
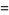 |
)/(k^2(2k; k))](http://mathworld.wolfram.com/images/equations/InverseSine/Inline66.gif) |
(20) |
![[sin^(-1)(1/2x)]^6](http://mathworld.wolfram.com/images/equations/InverseSine/Inline67.gif) |
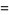 |
)/(k^2(2k; k))](http://mathworld.wolfram.com/images/equations/InverseSine/Inline69.gif) |
(21) |
![[sin^(-1)(1/2x)]^8](http://mathworld.wolfram.com/images/equations/InverseSine/Inline70.gif) |
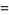 |
)/(k^2(2k; k))](http://mathworld.wolfram.com/images/equations/InverseSine/Inline72.gif) |
(22) |
(Bailey et al. 2007, pp. 16 and 282; Borwein and Chamberland 2007). Ramanujan gave the cases 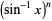 for
for 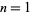 , 2, 3, and 4 (Berndt 1985, pp. 262-263), and the general cases are given in terms of multiple sums by Bailey et al. (2006, pp. 15-16 and 282) and Borwein and Chamberland (2007).
, 2, 3, and 4 (Berndt 1985, pp. 262-263), and the general cases are given in terms of multiple sums by Bailey et al. (2006, pp. 15-16 and 282) and Borwein and Chamberland (2007).
The inverse sine has continued fraction
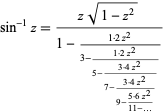 |
(23) |
(Wall 1948, p. 345).
REFERENCES:
Abramowitz, M. and Stegun, I. A.(Eds.). "Inverse Circular Functions." §4.4 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 79-83, 1972.
Apostol, T. M. Calculus, 2nd ed., Vol. 1: One-Variable Calculus, with an Introduction to Linear Algebra. Waltham, MA: Blaisdell, pp. 253-254, 1967.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Berndt, B. C. Ramanujan's Notebooks: Part I. New York: Springer-Verlag, 1985.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143 and 220, 1987.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Borwein, J. M. and Chamberland, M. "Integer Powers of Arcsin." Int. J. Math. Math. Sci., Art. 19381, 1-10, 2007.
Bronshtein, I. N. and Semendyayev, K. A. Handbook of Mathematics, 3rd ed. New York: Springer-Verlag, pp. 69-70, 1997.
GNU C Library. "Mathematics: Inverse Trigonometric Functions." http://www.gnu.org/manual/glibc-2.2.3/html_chapter/libc_19.html#SEC389.
Jeffrey, A. "Inverse Trigonometric and Hyperbolic Functions." §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 124-128, 2000.
Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science. New York: Springer-Verlag, p. 307, 1998.
Sloane, N. J. A. Sequences A002595/M4233 and A055786 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "Inverse Trigonometric Functions." Ch. 35 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 331-341, 1987.
Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.
Zwillinger, D.(Ed.). "Inverse Circular Functions." §6.3 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 465-467, 1995.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|