


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-9-2019
Date: 13-6-2019
Date: 29-9-2018
|
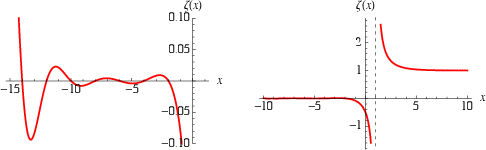
The Riemann zeta function is an extremely important special function of mathematics and physics that arises in definite integration and is intimately related with very deep results surrounding the prime number theorem. While many of the properties of this function have been investigated, there remain important fundamental conjectures (most notably the Riemann hypothesis) that remain unproved to this day. The Riemann zeta function is denoted  and is plotted above (using two different scales) along the real axis.
and is plotted above (using two different scales) along the real axis.
 |
In general,  is defined over the complex plane for one complex variable, which is conventionally denoted
is defined over the complex plane for one complex variable, which is conventionally denoted 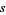 (instead of the usual
(instead of the usual 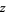 ) in deference to the notation used by Riemann in his 1859 paper that founded the study of this function (Riemann 1859).
) in deference to the notation used by Riemann in his 1859 paper that founded the study of this function (Riemann 1859).
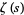 is implemented in the Wolfram Language as Zeta[s].
is implemented in the Wolfram Language as Zeta[s].
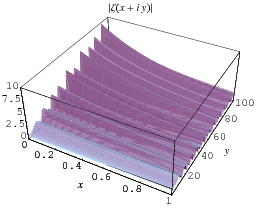
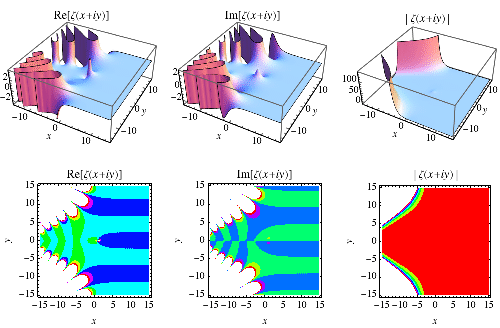
The plot above shows the "ridges" of 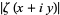 for
for 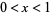 and
and 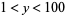 . The fact that the ridges appear to decrease monotonically for
. The fact that the ridges appear to decrease monotonically for 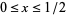 is not a coincidence since it turns out that monotonic decrease implies the Riemann hypothesis (Zvengrowski and Saidak 2003; Borwein and Bailey 2003, pp. 95-96).
is not a coincidence since it turns out that monotonic decrease implies the Riemann hypothesis (Zvengrowski and Saidak 2003; Borwein and Bailey 2003, pp. 95-96).
On the real line with 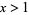 , the Riemann zeta function can be defined by the integral
, the Riemann zeta function can be defined by the integral
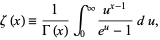 |
(1) |
where 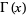 is the gamma function. If
is the gamma function. If  is an integer
is an integer 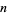 , then we have the identity
, then we have the identity
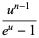 |
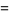 |
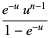 |
(2) |
 |
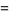 |
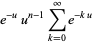 |
(3) |
 |
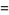 |
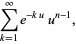 |
(4) |
so
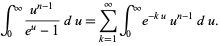 |
(5) |
To evaluate 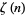 , let
, let 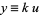 so that
so that 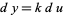 and plug in the above identity to obtain
and plug in the above identity to obtain
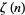 |
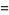 |
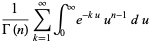 |
(6) |
 |
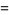 |
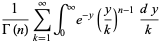 |
(7) |
 |
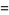 |
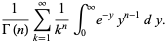 |
(8) |
Integrating the final expression in (8) gives 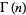 , which cancels the factor
, which cancels the factor 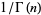 and gives the most common form of the Riemann zeta function,
and gives the most common form of the Riemann zeta function,
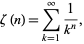 |
(9) |
which is sometimes known as a p-series.
The Riemann zeta function can also be defined in terms of multiple integrals by
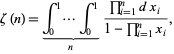 |
(10) |
and as a Mellin transform by
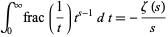 |
(11) |
for ![0<R[s]<1](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline37.gif) , where
, where 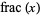 is the fractional part (Balazard and Saias 2000).
is the fractional part (Balazard and Saias 2000).
It appears in the unit square integral
![int_0^1int_0^1([-ln(xy)]^s)/(1-xy)dxdy=Gamma(s+2)zeta(s+2),](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/NumberedEquation6.gif) |
(12) |
valid for ![R[s]>1](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline39.gif) (Guillera and Sondow 2005). For
(Guillera and Sondow 2005). For 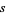 a nonnegative integer, this formula is due to Hadjicostas (2002), and the special cases
a nonnegative integer, this formula is due to Hadjicostas (2002), and the special cases 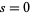 and
and 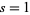 are due to Beukers (1979).
are due to Beukers (1979).
Note that the zeta function 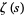 has a singularity at
has a singularity at 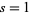 , where it reduces to the divergent harmonic series.
, where it reduces to the divergent harmonic series.
The Riemann zeta function satisfies the reflection functional equation
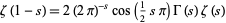 |
(13) |
(Hardy 1999, p. 14; Krantz 1999, p. 160), a similar form of which was conjectured by Euler for real 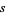 (Euler, read in 1749, published in 1768; Ayoub 1974; Havil 2003, p. 193). A symmetrical form of this functional equation is given by
(Euler, read in 1749, published in 1768; Ayoub 1974; Havil 2003, p. 193). A symmetrical form of this functional equation is given by
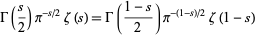 |
(14) |
(Ayoub 1974), which was proved by Riemann for all complex 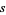 (Riemann 1859).
(Riemann 1859).
As defined above, the zeta function 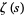 with
with 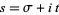 a complex number is defined for
a complex number is defined for ![R[s]>1](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline49.gif) . However,
. However, 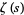 has a unique analytic continuation to the entire complex plane, excluding the point
has a unique analytic continuation to the entire complex plane, excluding the point 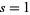 , which corresponds to a simple pole with complex residue 1 (Krantz 1999, p. 160). In particular, as
, which corresponds to a simple pole with complex residue 1 (Krantz 1999, p. 160). In particular, as 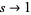 ,
, 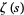 obeys
obeys
![lim_(s->1)[zeta(s)-1/(s-1)]=gamma,](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/NumberedEquation9.gif) |
(15) |
where 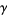 is the Euler-Mascheroni constant (Whittaker and Watson 1990, p. 271).
is the Euler-Mascheroni constant (Whittaker and Watson 1990, p. 271).
To perform the analytic continuation for ![R[s]>0](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline55.gif) , write
, write
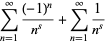 |
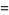 |
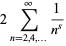 |
(16) |
 |
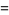 |
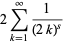 |
(17) |
 |
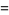 |
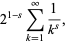 |
(18) |
so rewriting in terms of 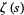 immediately gives
immediately gives
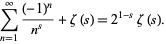 |
(19) |
Therefore,
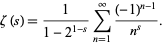 |
(20) |
Here, the sum on the right-hand side is exactly the Dirichlet eta function 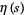 (sometimes also called the alternating zeta function). While this formula defines
(sometimes also called the alternating zeta function). While this formula defines 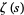 for only the right half-plane
for only the right half-plane ![R[s]>0](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline68.gif) , equation (◇) can be used to analytically continue it to the rest of the complex plane. Analytic continuation can also be performed using Hankel functions. A globally convergent series for the Riemann zeta function (which provides the analytic continuation of
, equation (◇) can be used to analytically continue it to the rest of the complex plane. Analytic continuation can also be performed using Hankel functions. A globally convergent series for the Riemann zeta function (which provides the analytic continuation of 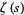 to the entire complex plane except
to the entire complex plane except 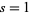 ) is given by
) is given by
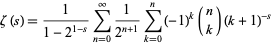 |
(21) |
(Havil 2003, p. 206), where 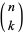 is a binomial coefficient, which was conjectured by Knopp around 1930, proved by Hasse (1930), and rediscovered by Sondow (1994). This equation is related to renormalization and random variates (Biane et al. 2001) and can be derived by applying Euler's series transformation with
is a binomial coefficient, which was conjectured by Knopp around 1930, proved by Hasse (1930), and rediscovered by Sondow (1994). This equation is related to renormalization and random variates (Biane et al. 2001) and can be derived by applying Euler's series transformation with 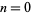 to equation (20).
to equation (20).
Hasse (1930) also proved the related globally (but more slowly) convergent series
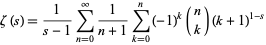 |
(22) |
that, unlike (21), can also be extended to a generalization of the Riemann zeta function known as the Hurwitz zeta function 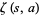 .
. 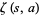 is defined such that
is defined such that
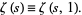 |
(23) |
(If the singular term is excluded from the sum definition of 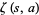 , then
, then 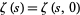 as well.) Expanding
as well.) Expanding 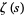 about
about 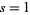 gives
gives
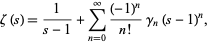 |
(24) |
where 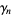 are the so-called Stieltjes constants.
are the so-called Stieltjes constants.
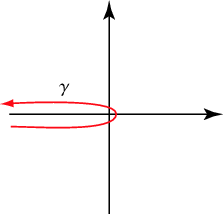
The Riemann zeta function can also be defined in the complex plane by the contour integral
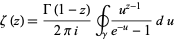 |
(25) |
for all 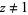 , where the contour is illustrated above (Havil 2003, pp. 193 and 249-252).
, where the contour is illustrated above (Havil 2003, pp. 193 and 249-252).
Zeros of 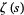 come in (at least) two different types. So-called "trivial zeros" occur at all negative even integers
come in (at least) two different types. So-called "trivial zeros" occur at all negative even integers  ,
, 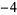 ,
, 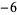 , ..., and "nontrivial zeros" at certain
, ..., and "nontrivial zeros" at certain
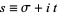 |
(26) |
for 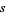 in the "critical strip"
in the "critical strip" 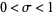 . The Riemann hypothesis asserts that the nontrivial Riemann zeta function zeros of
. The Riemann hypothesis asserts that the nontrivial Riemann zeta function zeros of 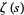 all have real part
all have real part ![sigma=R[s]=1/2](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline88.gif) , a line called the "critical line." This is now known to be true for the first
, a line called the "critical line." This is now known to be true for the first 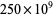 roots.
roots.
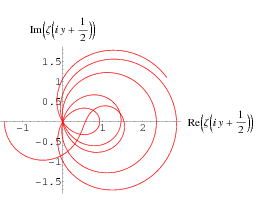
The plot above shows the real and imaginary parts of 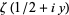 (i.e., values of
(i.e., values of 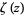 along the critical line) as
along the critical line) as 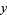 is varied from 0 to 35 (Derbyshire 2004, p. 221).
is varied from 0 to 35 (Derbyshire 2004, p. 221).
The Riemann zeta function can be split up into
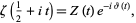 |
(27) |
where 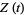 and
and 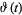 are the Riemann-Siegel functions.
are the Riemann-Siegel functions.
The Riemann zeta function is related to the Dirichlet lambda function 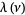 and Dirichlet eta function
and Dirichlet eta function 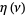 by
by
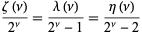 |
(28) |
and
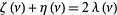 |
(29) |
(Spanier and Oldham 1987).
It is related to the Liouville function 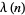 by
by
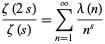 |
(30) |
(Lehman 1960, Hardy and Wright 1979). Furthermore,
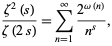 |
(31) |
where 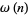 is the number of distinct prime factors of
is the number of distinct prime factors of 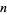 (Hardy and Wright 1979, p. 254).
(Hardy and Wright 1979, p. 254).
For 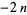 a positive even integer
a positive even integer 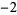 ,
, 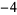 , ...,
, ...,
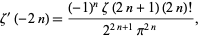 |
(32) |
giving the first few as
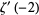 |
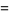 |
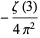 |
(33) |
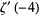 |
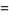 |
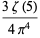 |
(34) |
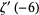 |
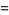 |
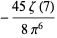 |
(35) |
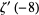 |
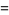 |
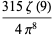 |
(36) |
(OEIS A117972 and A117973). For 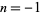 ,
,
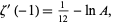 |
(37) |
where 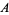 is the Glaisher-Kinkelin constant. Using equation (◇) gives the derivative
is the Glaisher-Kinkelin constant. Using equation (◇) gives the derivative
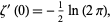 |
(38) |
which can be derived directly from the Wallis formula (Sondow 1994). 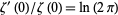 can also be derived directly from the Euler-Maclaurin summation formula (Edwards 2001, pp. 134-135). In general,
can also be derived directly from the Euler-Maclaurin summation formula (Edwards 2001, pp. 134-135). In general, 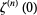 can be expressed analytically in terms of
can be expressed analytically in terms of 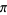 ,
, 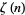 , the Euler-Mascheroni constant
, the Euler-Mascheroni constant 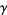 , and the Stieltjes constants
, and the Stieltjes constants 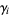 , with the first few examples being
, with the first few examples being
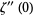 |
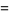 |
![gamma_1+1/2gamma^2-1/(24)pi^2-1/2[ln(2pi)]^2](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline125.gif) |
(39) |
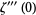 |
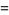 |
![3ln(2pi)gamma_1+3gammagamma_1+3/2gamma_2-zeta(3)-1/2[ln(2pi)]^3-1/8pi^2ln(2pi)+3/2gamma^2ln(2pi)+gamma^3.](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline128.gif) |
(40) |
Derivatives 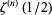 can also be given in closed form, for example,
can also be given in closed form, for example,
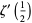 |
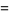 |
![1/4[(pi+2gamma+6ln2+2lnpi)zeta(1/2)]](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline132.gif) |
(41) |
 |
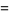 |
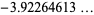 |
(42) |
(OEIS A114875).
The derivative of the Riemann zeta function for ![R[s]>1](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline136.gif) is defined by
is defined by
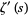 |
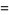 |
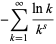 |
(43) |
 |
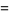 |
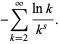 |
(44) |
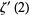 can be given in closed form as
can be given in closed form as
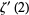 |
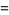 |
![1/6pi^2[gamma+ln(2pi)-12lnA]](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline146.gif) |
(45) |
 |
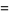 |
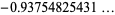 |
(46) |
(OEIS A073002), where 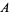 is the Glaisher-Kinkelin constant (given in series form by Glaisher 1894).
is the Glaisher-Kinkelin constant (given in series form by Glaisher 1894).
The series for 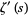 about
about 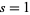 is
is
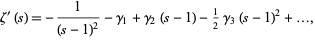 |
(47) |
where 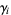 are Stieltjes constants.
are Stieltjes constants.
In 1739, Euler found the rational coefficients 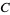 in
in 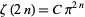 in terms of the Bernoulli numbers. Which, when combined with the 1882 proof by Lindemann that
in terms of the Bernoulli numbers. Which, when combined with the 1882 proof by Lindemann that 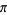 is transcendental, effectively proves that
is transcendental, effectively proves that 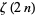 is transcendental. The study of
is transcendental. The study of 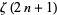 is significantly more difficult. Apéry (1979) finally proved
is significantly more difficult. Apéry (1979) finally proved 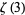 to be irrational, but no similar results are known for other odd
to be irrational, but no similar results are known for other odd 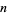 . As a result of Apéry's important discovery,
. As a result of Apéry's important discovery, 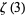 is sometimes called Apéry's constant. Rivoal (2000) and Ball and Rivoal (2001) proved that there are infinitely many integers
is sometimes called Apéry's constant. Rivoal (2000) and Ball and Rivoal (2001) proved that there are infinitely many integers 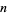 such that
such that 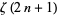 is irrational, and subsequently that at least one of
is irrational, and subsequently that at least one of 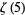 ,
, 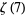 , ...,
, ..., 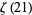 is irrational (Rivoal 2001). This result was subsequently tightened by Zudilin (2001), who showed that at least one of
is irrational (Rivoal 2001). This result was subsequently tightened by Zudilin (2001), who showed that at least one of 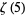 ,
, 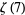 ,
, 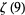 , or
, or 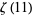 is irrational.
is irrational.
A number of interesting sums for 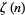 , with
, with 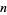 a positive integer, can be written in terms of binomial coefficients as the binomial sums
a positive integer, can be written in terms of binomial coefficients as the binomial sums
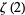 |
 |
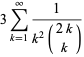 |
(48) |
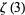 |
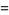 |
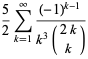 |
(49) |
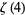 |
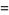 |
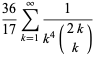 |
(50) |
(Guy 1994, p. 257; Bailey et al. 2007, p. 70). Apéry arrived at his result with the aid of the 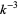 sum formula above. A relation of the form
sum formula above. A relation of the form
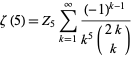 |
(51) |
has been searched for with 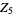 a rational or algebraic number, but if
a rational or algebraic number, but if 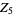 is a root of a polynomial of degree 25 or less, then the Euclidean norm of the coefficients must be larger than
is a root of a polynomial of degree 25 or less, then the Euclidean norm of the coefficients must be larger than 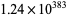 , and if
, and if 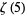 if algebraic of degree 25 or less, then the norm of coefficients must exceed
if algebraic of degree 25 or less, then the norm of coefficients must exceed 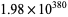 (Bailey et al. 2007, pp. 70-71, updating Bailey and Plouffe). Therefore, no such sums for
(Bailey et al. 2007, pp. 70-71, updating Bailey and Plouffe). Therefore, no such sums for 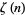 are known for
are known for 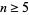 .
.
The identity
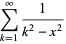 |
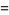 |
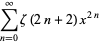 |
(52) |
 |
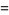 |
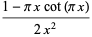 |
(53) |
 |
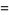 |
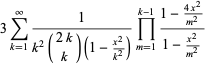 |
(54) |
 |
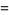 |
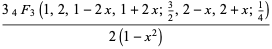 |
(55) |
for  is complex number not equal to a nonzero integer gives an Apéry-like formula for even positive
is complex number not equal to a nonzero integer gives an Apéry-like formula for even positive 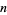 (Bailey et al. 2006, pp. 72-77).
(Bailey et al. 2006, pp. 72-77).
The Riemann zeta function 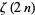 may be computed analytically for even
may be computed analytically for even 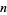 using either contour integration or Parseval's theorem with the appropriate Fourier series. An unexpected and important formula involving a product over the primes was first discovered by Euler in 1737,
using either contour integration or Parseval's theorem with the appropriate Fourier series. An unexpected and important formula involving a product over the primes was first discovered by Euler in 1737,
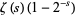 |
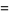 |
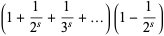 |
(56) |
 |
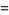 |
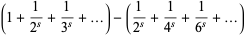 |
(57) |
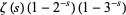 |
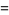 |
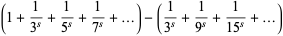 |
(58) |
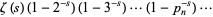 |
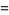 |
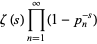 |
(59) |
 |
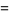 |
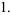 |
(60) |
Here, each subsequent multiplication by the 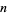 th prime
th prime 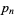 leaves only terms that are powers of
leaves only terms that are powers of 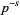 . Therefore,
. Therefore,
![zeta(s)=[product_(n=1)^infty(1-p_n^(-s))]^(-1),](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/NumberedEquation28.gif) |
(61) |
which is known as the Euler product formula (Hardy 1999, p. 18; Krantz 1999, p. 159), and called "the golden key" by Derbyshire (2004, pp. 104-106). The formula can also be written
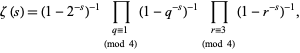 |
(62) |
where 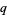 and
and 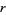 are the primes congruent to 1 and 3 modulo 4, respectively.
are the primes congruent to 1 and 3 modulo 4, respectively.
For even 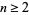 ,
,
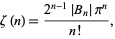 |
(63) |
where 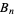 is a Bernoulli number (Mathews and Walker 1970, pp. 50-53; Havil 2003, p. 194). Another intimate connection with the Bernoulli numbers is provided by
is a Bernoulli number (Mathews and Walker 1970, pp. 50-53; Havil 2003, p. 194). Another intimate connection with the Bernoulli numbers is provided by
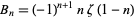 |
(64) |
for 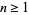 , which can be written
, which can be written
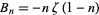 |
(65) |
for 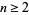 . (In both cases, only the even cases are of interest since
. (In both cases, only the even cases are of interest since 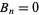 trivially for odd
trivially for odd 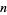 .) Rewriting (65),
.) Rewriting (65),
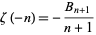 |
(66) |
for 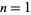 , 3, ... (Havil 2003, p. 194), where
, 3, ... (Havil 2003, p. 194), where 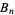 is a Bernoulli number, the first few values of which are
is a Bernoulli number, the first few values of which are 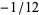 , 1/120,
, 1/120, 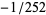 , 1/240, ... (OEIS A001067 and A006953).
, 1/240, ... (OEIS A001067 and A006953).
Although no analytic form for 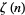 is known for odd
is known for odd 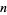 ,
,
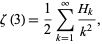 |
(67) |
where 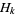 is a harmonic number (Stark 1974). In addition,
is a harmonic number (Stark 1974). In addition, 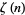 can be expressed as the sum limit
can be expressed as the sum limit
![zeta(n)=lim_(x->infty)1/((2x+1)^n)sum_(k=1)^x[cot(k/(2x+1))]^n](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/NumberedEquation35.gif) |
(68) |
for 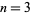 , 5, ... (Apostol 1973, given incorrectly in Stark 1974).
, 5, ... (Apostol 1973, given incorrectly in Stark 1974).
For 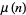 the Möbius function,
the Möbius function,
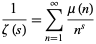 |
(69) |
(Havil 2003, p. 209).
The values of 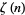 for small positive integer values of
for small positive integer values of 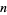 are
are
 |
 |
 |
(70) |
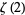 |
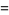 |
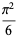 |
(71) |
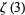 |
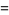 |
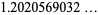 |
(72) |
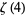 |
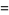 |
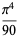 |
(73) |
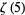 |
 |
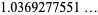 |
(74) |
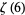 |
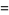 |
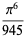 |
(75) |
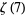 |
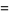 |
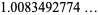 |
(76) |
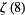 |
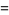 |
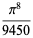 |
(77) |
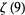 |
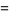 |
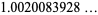 |
(78) |
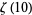 |
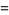 |
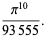 |
(79) |
Euler gave 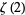 to
to 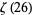 for even
for even 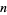 (Wells 1986, p. 54), and Stieltjes (1993) determined the values of
(Wells 1986, p. 54), and Stieltjes (1993) determined the values of 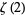 , ...,
, ..., 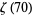 to 30 digits of accuracy in 1887. The denominators of
to 30 digits of accuracy in 1887. The denominators of 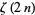 for
for 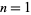 , 2, ... are 6, 90, 945, 9450, 93555, 638512875, ... (OEIS A002432). The numbers of decimal digits in the denominators of
, 2, ... are 6, 90, 945, 9450, 93555, 638512875, ... (OEIS A002432). The numbers of decimal digits in the denominators of 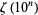 for
for 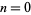 , 1, ... are 1, 5, 133, 2277, 32660, 426486, 5264705, ... (OEIS A114474).
, 1, ... are 1, 5, 133, 2277, 32660, 426486, 5264705, ... (OEIS A114474).
An integral for positive even integers is given by
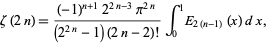 |
(80) |
and integrals for positive odd integers are given by
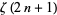 |
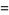 |
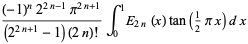 |
(81) |
 |
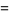 |
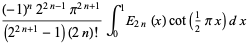 |
(82) |
 |
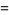 |
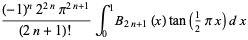 |
(83) |
 |
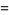 |
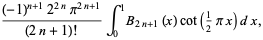 |
(84) |
where 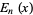 is an Euler polynomial and
is an Euler polynomial and 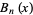 is a Bernoulli polynomial (Cvijović and Klinowski 2002; J. Crepps, pers. comm., Apr. 2002).
is a Bernoulli polynomial (Cvijović and Klinowski 2002; J. Crepps, pers. comm., Apr. 2002).
The value of 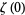 can be computed by performing the inner sum in equation (◇) with
can be computed by performing the inner sum in equation (◇) with 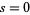 ,
,
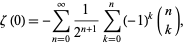 |
(85) |
to obtain
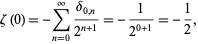 |
(86) |
where 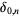 is the Kronecker delta.
is the Kronecker delta.
Similarly, the value of 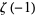 can be computed by performing the inner sum in equation (◇) with
can be computed by performing the inner sum in equation (◇) with 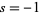 ,
,
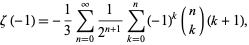 |
(87) |
which gives
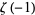 |
 |
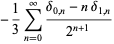 |
(88) |
 |
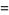 |
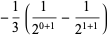 |
(89) |
 |
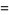 |
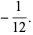 |
(90) |
This value is related to a deep result in renormalization theory (Elizalde et al. 1994, 1995, Bloch 1996, Lepowski 1999).
It is apparently not known if the value
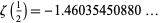 |
(91) |
(OEIS A059750) can be expressed in terms of known mathematical constants. This constant appears, for example, in Knuth's series.
Rapidly converging series for 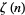 for
for 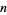 odd were first discovered by Ramanujan (Zucker 1979, 1984, Berndt 1988, Bailey et al. 1997, Cohen 2000). For
odd were first discovered by Ramanujan (Zucker 1979, 1984, Berndt 1988, Bailey et al. 1997, Cohen 2000). For 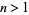 and
and 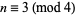 ,
,
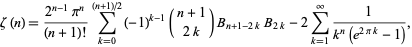 |
(92) |
where 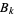 is again a Bernoulli number and
is again a Bernoulli number and 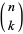 is a binomial coefficient. The values of the left-hand sums (divided by
is a binomial coefficient. The values of the left-hand sums (divided by 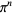 ) in (92) for
) in (92) for 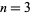 , 7, 11, ... are 7/180, 19/56700, 1453/425675250, 13687/390769879500, 7708537/21438612514068750, ... (OEIS A057866 and A057867). For
, 7, 11, ... are 7/180, 19/56700, 1453/425675250, 13687/390769879500, 7708537/21438612514068750, ... (OEIS A057866 and A057867). For 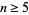 and
and 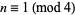 , the corresponding formula is slightly messier,
, the corresponding formula is slightly messier,
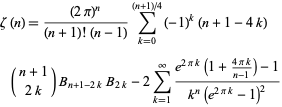 |
(93) |
(Cohen 2000).
Defining
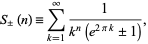 |
(94) |
the first few values can then be written
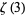 |
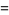 |
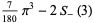 |
(95) |
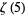 |
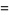 |
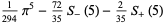 |
(96) |
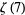 |
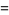 |
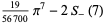 |
(97) |
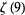 |
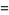 |
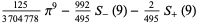 |
(98) |
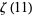 |
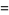 |
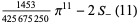 |
(99) |
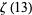 |
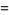 |
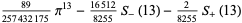 |
(100) |
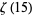 |
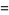 |
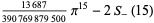 |
(101) |
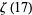 |
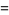 |
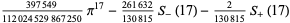 |
(102) |
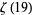 |
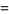 |
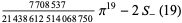 |
(103) |
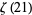 |
 |
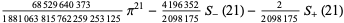 |
(104) |
(Plouffe 1998).
Another set of related formulas are
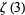 |
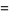 |
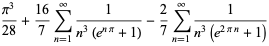 |
(105) |
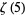 |
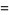 |
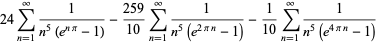 |
(106) |
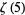 |
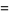 |
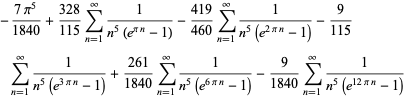 |
(107) |
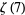 |
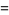 |
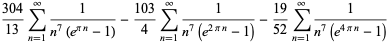 |
(108) |
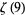 |
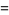 |
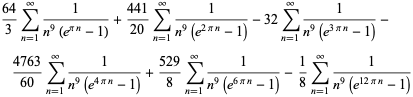 |
(109) |
(Plouffe 2006).
Multiterm sums for odd 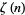 include
include
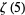 |
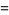 |
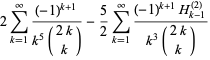 |
(110) |
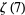 |
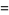 |
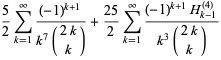 |
(111) |
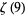 |
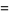 |
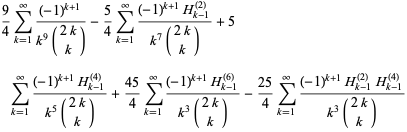 |
(112) |
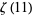 |
 |
![5/2sum_(k=1)^(infty)((-1)^(k+1))/(k^(11)(2k; k))+(25)/2sum_(k=1)^(infty)((-1)^(k+1)H_(k-1)^((4)))/(k^7(2k; k))-(75)/4sum_(k=1)^(infty)((-1)^(k+1)H_(k-1)^((8)))/(k^3(2k; k))+(125)/4sum_(k=1)^(infty)((-1)^(k+1)[H_(k-1)^((4))]^2)/(k^3(2k; k))](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline378.gif) |
(113) |
(Borwein and Bradley 1996, 1997; Bailey et al. 2007, p. 71), where 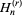 is a generalized harmonic number.
is a generalized harmonic number.
G. Huvent (2002) found the beautiful formula
![zeta(5)=-(16)/(11)sum_(n=1)^infty([2(-1)^n+1]H_n)/(n^4).](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/NumberedEquation45.gif) |
(114) |
A number of sum identities involving 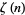 include
include
![sum_(n=2)^(infty)[zeta(n)-1]](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline381.gif) |
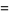 |
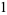 |
(115) |
![sum_(n=2,4,...)^(infty)[zeta(n)-1]](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline384.gif) |
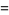 |
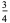 |
(116) |
![sum_(n=3,5,...)^(infty)[zeta(n)-1]](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline387.gif) |
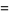 |
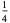 |
(117) |
![sum_(n=2)^(infty)(-1)^n[zeta(n)-1]](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline390.gif) |
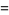 |
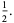 |
(118) |
Sums involving integers multiples of the argument include
![sum_(n=1)^(infty)[zeta(2n)-1]](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline393.gif) |
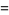 |
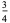 |
(119) |
![sum_(n=1)^(infty)[zeta(3n)-1]](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline396.gif) |
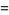 |
![1/3[-(-1)^(2/3)H_((3-isqrt(3))/2)+(-1)^(1/3)H_((3+isqrt(3))/2)]](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline398.gif) |
(120) |
![sum_(n=1)^(infty)[zeta(4n)-1]](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/Inline399.gif) |
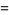 |
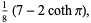 |
(121) |
where 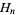 is a harmonic number.
is a harmonic number.
Two surprising sums involving 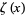 are given by
are given by
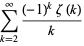 |
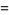 |
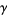 |
(122) |
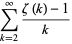 |
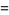 |
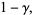 |
(123) |
where 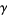 is the Euler-Mascheroni constant (Havil 2003, pp. 109 and 111-112). Equation (122) can be generalized to
is the Euler-Mascheroni constant (Havil 2003, pp. 109 and 111-112). Equation (122) can be generalized to
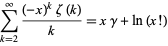 |
(124) |
(T. Drane, pers. comm., Jul. 7, 2006) for 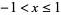 .
.
Other unexpected sums are
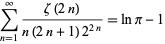 |
(125) |
(Tyler and Chernhoff 1985; Boros and Moll 2004, p. 248) and
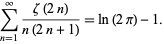 |
(126) |
(125) is a special case of
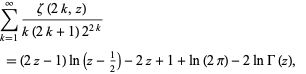 |
(127) |
where 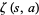 is a Hurwitz zeta function (Danese 1967; Boros and Moll 2004, p. 248).
is a Hurwitz zeta function (Danese 1967; Boros and Moll 2004, p. 248).
Considering the sum
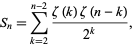 |
(128) |
then
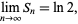 |
(129) |
where 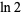 is the natural logarithm of 2, which is a particular case of
is the natural logarithm of 2, which is a particular case of
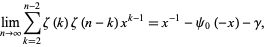 |
(130) |
where 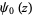 is the digamma function and
is the digamma function and 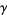 is the Euler-Mascheroni constant, which can be derived from
is the Euler-Mascheroni constant, which can be derived from
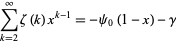 |
(131) |
(B. Cloitre, pers. comm., Dec. 11, 2005; cf. Borwein et al. 2000, eqn. 27).
A generalization of a result of Ramanujan (who gave the  case) is given by
case) is given by
![sum_(k=1)^infty1/([k(k+1)]^(2m+1))=-2sum_(k=0)^mzeta(2k)(4m-2k+1; 2m),](http://mathworld.wolfram.com/images/equations/RiemannZetaFunction/NumberedEquation54.gif) |
(132) |
where 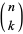 is a binomial coefficient (B. Cloitre, pers. comm., Sep. 20, 2005).
is a binomial coefficient (B. Cloitre, pers. comm., Sep. 20, 2005).
An additional set of sums over 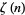 is given by
is given by
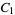 |
 |
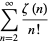 |
(133) |
 |
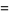 |
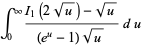 |
(134) |
 |
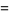 |
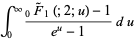 |
(135) |
 |
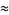 |
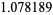 |
(136) |
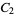 |
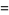 |
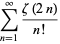 |
(137) |
 |
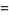 |
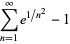 |
(138) |
 |
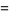 |
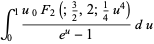 |
(139) |
 |
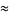 |
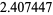 |
(140) |
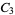 |
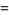 |
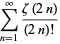 |
(141) |
 |
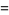 |
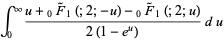 |
(142) |
 |
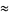 |
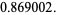 |
(143) |
(OEIS A093720, A076813, and A093721), where 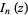 is a modified Bessel function of the first kind,
is a modified Bessel function of the first kind, 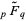 is a regularized hypergeometric function. These sums have no known closed-form expression.
is a regularized hypergeometric function. These sums have no known closed-form expression.
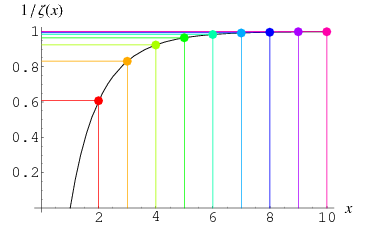
The inverse of the Riemann zeta function 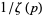 , plotted above, is the asymptotic density of
, plotted above, is the asymptotic density of 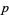 th-powerfree numbers (i.e., squarefree numbers, cubefree numbers, etc.). The following table gives the number
th-powerfree numbers (i.e., squarefree numbers, cubefree numbers, etc.). The following table gives the number 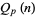 of
of 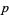 th-powerfree numbers
th-powerfree numbers 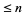 for several values of
for several values of 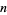 .
.
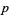 |
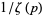 |
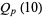 |
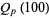 |
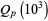 |
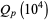 |
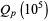 |
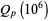 |
| 2 | 0.607927 | 7 | 61 | 608 | 6083 | 60794 | 607926 |
| 3 | 0.831907 | 9 | 85 | 833 | 8319 | 83190 | 831910 |
| 4 | 0.923938 | 10 | 93 | 925 | 9240 | 92395 | 923939 |
| 5 | 0.964387 | 10 | 97 | 965 | 9645 | 96440 | 964388 |
| 6 | 0.982953 | 10 | 99 | 984 | 9831 | 98297 | 982954 |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Riemann Zeta Function and Other Sums of Reciprocal Powers." §23.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 807-808, 1972.
Adamchik, V. S. and Srivastava, H. M. "Some Series of the Zeta and Related Functions." Analysis 18, 131-144, 1998.
Aizenberg, L.; Adamchik, V.; and Levit, V. E. "Approaching the Riemann Hypothesis with Mathematica." http://library.wolfram.com/infocenter/Articles/3268/.
Apéry, R. "Irrationalité de 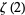 et
et 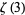 ." Astérisque 61, 11-13, 1979.
." Astérisque 61, 11-13, 1979.
Apostol, T. M. "Another Elementary Proof of Euler's Formula for 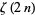 ." Amer. Math. Monthly 80, 425-431, 1973.
." Amer. Math. Monthly 80, 425-431, 1973.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 332-335, 1985.
Ayoub, R. "Euler and the Zeta Function." Amer. Math. Monthly 81, 1067-1086, 1974.
Bailey, D. H. "Multiprecision Translation and Execution of Fortran Programs." ACM Trans. Math. Software. To appear.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Bailey, D. H.; Borwein, J. M.; and Crandall, R. E. "On the Khinchin Constant." Math. Comput. 66, 417-431, 1997.
Bailey, D. and Plouffe, S. "Recognizing Numerical Constants." http://www.cecm.sfu.ca/organics/papers/bailey/.
Balazard, M. and Saias, E. "The Nyman-Beurling Equivalent Form for the Riemann Hypothesis." Expos. Math. 18, 131-138, 2000.
Balazard, M.; Saias, E.; and Yor, M. "Notes sur la fonction 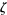 de Riemann, 2." Adv. Math. 143, 284-287, 1999.
de Riemann, 2." Adv. Math. 143, 284-287, 1999.
Ball, K. and Rivoal, T. "Irrationalité d'une infinité valeurs de la fonction zêta aux entiers impairs." Invent. Math. 146, 193-207, 2001.
Berndt, B. C. Ch. 14 in Ramanujan's Notebooks, Part II. New York: Springer-Verlag, 1988.
Beukers, F. "A Note on the Irrationality of 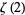 and
and 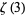 ." Bull. London Math. Soc. 11, 268-272, 1979.
." Bull. London Math. Soc. 11, 268-272, 1979.
Biane, P.; Pitman, J.; and Yor, M. "Probability Laws Related to the Jacobi Theta and Riemann Zeta Functions, and Brownian Excursions." Bull. Amer. Math. Soc. 38, 435-465, 2001.
Bloch, S. "Zeta Values and Differential Operators on the Circle." J. Algebra 182, 476-500, 1996.
Boros, G. and Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 95-96 and 99-100, 2003.
Borwein, D. and Borwein, J. "On an Intriguing Integral and Some Series Related to 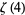 ." Proc. Amer. Math. Soc. 123, 1191-1198, 1995.
." Proc. Amer. Math. Soc. 123, 1191-1198, 1995.
Borwein, J. M. and Bradley, D. M. "Searching Symbolically for Apéry-Like Formulae for Values of the Riemann Zeta Function." ACM SIGSAM Bull. Algebraic Sym. Manip. 30, 2-7, 1996.
Borwein, J. M. and Bradley, D. M. "Empirically Determined Apéry-Like Formulae for 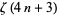 ." Exp. Math. 6, 181-194, 1997.
." Exp. Math. 6, 181-194, 1997.
Borwein, J. M.; Bradley, D. M.; and Crandall, R. E. "Computational Strategies for the Riemann Zeta Function." J. Comput. Appl. Math. 121, 247-296, 2000.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988.
Choudhury, B. K. "The Riemann Zeta-Function and Its Derivatives." Proc. Roy. Soc. London Ser. A 450, 477-499, 1995.
Cohen, H. "High Precision Computation of Hardy-Littlewood Constants." Preprint. http://www.math.u-bordeaux.fr/~cohen/hardylw.dvi. 2000.
Conrey, J. B. "The Riemann Hypothesis." Not. Amer. Math. Soc. 50, 341-353, 2003. http://www.ams.org/notices/200303/fea-conrey-web.pdf.
Cvijović, D. and Klinowski, J. "Integral Representations of the Riemann Zeta Function for Odd-Integer Arguments." J. Comput. Appl. Math. 142, 435-439, 2002.
Danese, A. E. "Solution to Problem 1801. A Zeta-Function Identity." Amer. Math. Monthly 74, 80-81, 1967.
Davenport, H. Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, 1980.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.
Elizalde, E. Ten Physical Applications of Spectral Zeta Functions. Berlin: Springer-Verlag, 1995.
Elizalde, E.; Odintsov, S. D.; Romeo, A.; Bytsenko, A. A.; and Zerbini, S. Zeta Regularization Techniques With Applications. River Edge, NJ: World Scientific, 1994.
Euler, L. "Remarques sur un beau rapport entre les series des puissances tant directes que réciproques." Mémoires de l'academie des sciences de Berlin 17, 83-106, 1768. Reprinted in Opera Omnia, Series 1, Vol. 15 pp. 70-90.
Glaisher, J. W. L. "On the Constant which Occurs in the Formula for 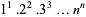 ." Messenger Math. 24, 1-16, 1894.
." Messenger Math. 24, 1-16, 1894.
Guillera, J. and Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005 http://arxiv.org/abs/math.NT/0506319.
Guy, R. K. "Series Associated with the 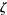 -Function." §F17 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 257-258, 1994.
-Function." §F17 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 257-258, 1994.
Hadjicostas, P. "Some Generalizations of Beukers' Integrals." Kyungpook Math. J. 42, 399-416, 2002.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Wright, E. M. "The Zeta Function." §17.2 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 245-247 and 255, 1979.
Hasse, H. "Ein Summierungsverfahren für die Riemannsche Zeta-Reihe." Math. Z. 32, 458-464, 1930.
Hauss, M. Verallgemeinerte Stirling, Bernoulli und Euler Zahlen, deren Anwendungen und schnell konvergente Reihen für Zeta Funktionen. Aachen, Germany: Verlag Shaker, 1995.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Howson, A. G. "Addendum to: 'Euler and the Zeta Function' (Amer. Math. Monthly 81 (1974), 1067-1086) by Raymond Ayoub." Amer. Math. Monthly 82, 737, 1975.
Huvent, G. "Autour de la primitive de 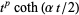 ." Feb. 3, 2002. http://perso.orange.fr/gery.huvent/articlespdf/Autour_primitive.pdf.
." Feb. 3, 2002. http://perso.orange.fr/gery.huvent/articlespdf/Autour_primitive.pdf.
Huylebrouck, D. "Similarities in Irrationality Proofs for 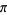 ,
, 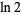 ,
, 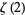 , and
, and 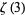 ." Amer. Math. Monthly 108, 222-231, 2001.
." Amer. Math. Monthly 108, 222-231, 2001.
Ivic, A. A. The Riemann Zeta-Function. New York: Wiley, 1985.
Ivic, A. A. Lectures on Mean Values of the Riemann Zeta Function. Berlin: Springer-Verlag, 1991.
Jones, G. A. and Jones, J. M. "The Riemann Zeta Function." Ch. 9 in Elementary Number Theory. Berlin: Springer-Verlag, pp. 163-189, 1998.
Karatsuba, A. A. and Voronin, S. M. The Riemann Zeta-Function. Hawthorne, NY: De Gruyter, 1992.
Katayama, K. "On Ramanujan's Formula for Values of Riemann Zeta-Function at Positive Odd Integers." Acta Math. 22, 149-155, 1973.
Keiper, J. "The Zeta Function of Riemann." Mathematica Educ. Res. 4, 5-7, 1995.
Knopp, K. "4th Example: The Riemann 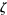 -Function." Theory of Functions Parts I and II, Two Volumes Bound as One, Part II. New York: Dover, pp. 51-57, 1996.
-Function." Theory of Functions Parts I and II, Two Volumes Bound as One, Part II. New York: Dover, pp. 51-57, 1996.
Krantz, S. G. "Riemann's Zeta Function." §13.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 158-159, 1999.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 35, 1983.
Lehman, R. S. "On Liouville's Function." Math. Comput. 14, 311-320, 1960.
Lepowski, J. "Vertex Operator Algebras and the Zeta Function." 29 Sep 1999. http://arxiv.org/abs/math.QA/9909178.
Mathews, J. and Walker, R. L. Mathematical Methods of Physics, 2nd ed. Reading, MA: W. A. Benjamin/Addison-Wesley, pp. 50-53, 1970.
Patterson, S. J. An Introduction to the Theory of the Riemann Zeta-Function. New York: Cambridge University Press, 1988.
Pegg, E. Jr. and Weisstein, E. W. "Seven Mathematical Tidbits." MathWorld Headline News. Nov. 8, 2004. http://mathworld.wolfram.com/news/2004-11-08/seventidbits/#3.
Plouffe, S. "Identities Inspired from Ramanujan Notebooks II." Jul. 21, 1998. http://www.lacim.uqam.ca/~plouffe/identities.html.
Plouffe, S. "Identities Inspired from Ramanujan Notebooks (Part 2)." Apr. 2006. http://www.lacim.uqam.ca/~plouffe/inspired2.pdf.
Riemann, G. F. B. "Über die Anzahl der Primzahlen unter einer gegebenen Grösse." Monatsber. Königl. Preuss. Akad. Wiss. Berlin, 671-680, Nov. 1859. Reprinted in Das Kontinuum und Andere Monographen (Ed. H. Weyl). New York: Chelsea, 1972.
Rivoal, T. "La fonction Zeta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs." Comptes Rendus Acad. Sci. Paris 331, 267-270, 2000.
Rivoal, T. "Irrationalité d'au moins un des neuf nombres 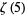 ,
, 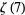 , ...,
, ..., 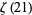 ." 25 Apr 2001. http://arxiv.org/abs/math.NT/0104221.
." 25 Apr 2001. http://arxiv.org/abs/math.NT/0104221.
Sloane, N. J. A. Sequences A001067, A002432/M4283, A006953/M2039, A057866, A057867, A059750, A073002, A076813, A093720, A093721, A114474, A114875, A117972, and A117973 in "The On-Line Encyclopedia of Integer Sequences."
Sondow, J. "Analytic Continuation of Riemann's Zeta Function and Values at Negative Integers via Euler's Transformation of Series." Proc. Amer. Math. Soc. 120, 421-424, 1994.
Spanier, J. and Oldham, K. B. "The Zeta Numbers and Related Functions." Ch. 3 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 25-33, 1987.
Srivastava, H. M. "Some Simple Algorithms for the Evaluations and Representations of the Riemann Zeta Function at Positive Integer Arguments." J. Math. Anal. Appl. 246, 331-351, 2000.
Stark, E. L. "The Series 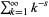
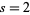 , 3, 4, ..., Once More." Math. Mag. 47, 197-202, 1974.
, 3, 4, ..., Once More." Math. Mag. 47, 197-202, 1974.
Stieltjes, T. J. Oeuvres Complètes, Vol. 2 (Ed. G. van Dijk.) New York: Springer-Verlag, p. 100, 1993.
Titchmarsh, E. C. The Zeta-Function of Riemann. London: Cambridge University Press, 1930.
Titchmarsh, E. C. The Theory of the Riemann Zeta Function, 2nd ed. New York: Clarendon Press, 1987.
Tyler, D. and Chernhoff, P. "Problem 3103. An Odd Sum Reappears." Amer. Math. Monthly 92, 507, 1985.
Vardi, I. "The Riemann Zeta Function." Ch. 8 in Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 141-174, 1991.
Wagon, S. "The Riemann Zeta Function." §10.6 in Mathematica in Action. New York: W. H. Freeman, pp. 353-362, 1991.
Watkins,M. R. "Inexplicable Secrets of Creation." http://www.maths.ex.ac.uk/~mwatkins/zeta/.
Weisstein, E. W. "Books about Riemann Zeta Function." http://www.ericweisstein.com/encyclopedias/books/RiemannZetaFunction.html.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Woon, S. C. "Generalization of a Relation Between the Riemann Zeta Function and Bernoulli Numbers." 24 Dec 1998. http://arxiv.org/abs/math.NT/9812143.
Zucker, I. J. "The Summation of Series of Hyperbolic Functions." SIAM J. Math. Anal. 10, 192-206, 1979.
Zucker, I. J. "Some Infinite Series of Exponential and Hyperbolic Functions." SIAM J. Math. Anal. 15, 406-413, 1984.
Zudilin, W. "One of the Numbers 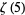 ,
, 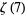 ,
, 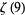 ,
, 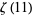 Is Irrational." Uspekhi Mat. Nauk 56, 149-150, 2001.
Is Irrational." Uspekhi Mat. Nauk 56, 149-150, 2001.
Zvengrowski, P. and Saidak, F. "On the Modulus of the Riemann Zeta Function in the Critical Strip." Math. Slovaca 53, 145-172, 2003.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
ضمن أسبوع الإرشاد النفسي.. جامعة العميد تُقيم أنشطةً ثقافية وتطويرية لطلبتها
|
|
|