


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-9-2019
Date: 25-3-2019
Date: 19-7-2019
|
Newton's iteration is an algorithm for computing the square root 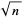 of a number
of a number 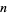 via the recurrence equation
via the recurrence equation
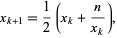 |
(1) |
where 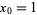 . This recurrence converges quadratically as
. This recurrence converges quadratically as 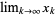 .
.
Newton's iteration is simply an application of Newton's method for solving the equation
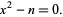 |
(2) |
For example, when applied numerically, the first few iterations to Pythagoras's constant 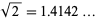 are 1, 1.5, 1.41667, 1.41422, 1.41421, ....
are 1, 1.5, 1.41667, 1.41422, 1.41421, ....
The first few approximants 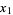 ,
, 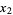 , ... to
, ... to 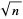 are given by
are given by
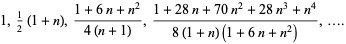 |
(3) |
These can be given by the analytic formula
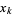 |
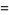 |
![sqrt(n)[1+2/(((1+sqrt(n))/(1-sqrt(n)))^(2^k)-1)]](http://mathworld.wolfram.com/images/equations/NewtonsIteration/Inline11.gif) |
(4) |
 |
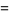 |
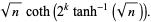 |
(5) |
These can be derived by noting that the recurrence can be written as
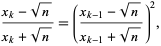 |
(6) |
which has the clever closed-form solution
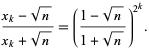 |
(7) |
Solving for 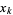 then gives the solution derived above.
then gives the solution derived above.
The following table summarizes the first few convergents for small positive integer 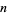
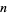 |
OEIS | 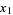 , , 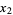 , ... , ... |
| 1 | 1, 1, 1, 1, 1, 1, 1, 1, ... | |
| 2 | A001601/A051009 | 1, 3/2, 17/12, 577/408, 665857/470832, ... |
| 3 | A002812/A071579 | 1, 2, 7/4, 97/56, 18817/10864, 708158977/408855776, ... |
REFERENCES:
Sloane, N. J. A. Sequences A001601/M3042, A002812/M1817, A051009, A071579 in "The On-Line Encyclopedia of Integer Sequences."
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 913, 2002.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
المجمع العلمي يواصل إقامة دوراته القرآنية لطلبة العلوم الدينية في النجف الأشرف
|
|
|