


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-10-2019
Date: 23-6-2019
Date: 29-9-2018
|
The 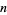 th root (or "
th root (or "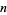 th radical") of a quantity
th radical") of a quantity 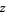 is a value
is a value 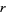 such that
such that 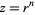 , and therefore is the inverse function to the taking of a power. The
, and therefore is the inverse function to the taking of a power. The 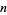 th root is denoted
th root is denoted ![r=RadicalBox[z, n]](http://mathworld.wolfram.com/images/equations/nthRoot/Inline7.gif) or, using power notation,
or, using power notation, 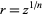 . The special case of the square root (
. The special case of the square root (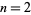 ) is denoted
) is denoted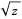 . The case
. The case 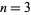 is known as the cube root.
is known as the cube root.
The quantities for which a general function equals 0 are also called roots, or sometimes zeros.
The quantities 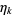 such that
such that 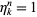 are called the
are called the 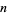 th roots of unity.
th roots of unity.
Rolle proved that any complex number has exactly 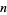
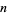 th roots (Boyer 1968, p. 476), though some are possibly degenerate. However, since complex numbers have two square roots and three cube roots, care is needed in determining which root is under consideration. For complex numbers
th roots (Boyer 1968, p. 476), though some are possibly degenerate. However, since complex numbers have two square roots and three cube roots, care is needed in determining which root is under consideration. For complex numbers 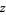 , the root of interest (generally taken as the root having smallest positive complex argument) is known as the principal root. However, for real numbers, the root of interest is usually the root that is real (when it exists).
, the root of interest (generally taken as the root having smallest positive complex argument) is known as the principal root. However, for real numbers, the root of interest is usually the root that is real (when it exists).
The principal 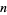 th root of a complex number
th root of a complex number 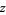 can be found in the Wolfram Language as z^(1/n) or equivalently Power[z, 1/n]. When only real roots are of interest, the command Surd[x, n] which returns the real-valued
can be found in the Wolfram Language as z^(1/n) or equivalently Power[z, 1/n]. When only real roots are of interest, the command Surd[x, n] which returns the real-valued 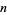 th root for real
th root for real  odd
odd 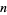 and the principal
and the principal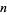 th root for nonnegative real
th root for nonnegative real  and even
and even 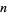 can be used.
can be used.
The 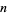 th root
th root 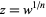 of a complex number
of a complex number 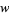 can be found analytically by solving the equation
can be found analytically by solving the equation
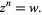 |
(1) |
Writing the 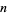 th power of a complex number
th power of a complex number 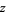 in terms of its norm and phase gives
in terms of its norm and phase gives
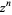 |
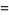 |
![|z|^n[cos(ntheta)+isin(ntheta)]](http://mathworld.wolfram.com/images/equations/nthRoot/Inline33.gif) |
(2) |
 |
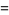 |
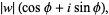 |
(3) |
so the roots have complex modulus
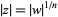 |
(4) |
and complex argument
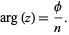 |



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
بالصور: ممثل المرجعية العليا الشيخ عبد المهدي الكربلائي يؤم جموع المؤمنين في صلاة عيد الفطر المبارك داخل الصحن الحسيني الشريف
|
|
|