


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-5-2019
Date: 25-8-2018
Date: 7-9-2019
|
The logarithm 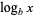 for a base
for a base 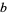 and a number
and a number  is defined to be the inverse function of taking
is defined to be the inverse function of taking 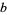 to the power
to the power  , i.e.,
, i.e., 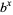 . Therefore, for any
. Therefore, for any  and
and 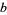 ,
,
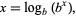 |
(1) |
or equivalently,
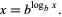 |
(2) |

For any base, the logarithm function has a singularity at 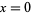 . In the above plot, the blue curve is the logarithm to base 2 (
. In the above plot, the blue curve is the logarithm to base 2 (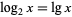 ), the black curve is the logarithm to base
), the black curve is the logarithm to base 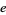 (the natural logarithm
(the natural logarithm 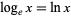 ), and the red curve is the logarithm to base10 (the common logarithm, i.e.,
), and the red curve is the logarithm to base10 (the common logarithm, i.e., 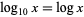 ).
).
Note that while logarithm base 10 is denoted 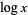 in this work, on calculators, and in elementary algebra and calculus textbooks, mathematicians and advanced mathematics texts uniformly use the notation
in this work, on calculators, and in elementary algebra and calculus textbooks, mathematicians and advanced mathematics texts uniformly use the notation 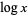 to mean
to mean 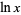 , and therefore use
, and therefore use 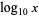 to mean the common logarithm. Extreme care is therefore needed when consulting the literature.
to mean the common logarithm. Extreme care is therefore needed when consulting the literature.
The situation is complicated even more by the fact that number theorists (e.g., Ivić 2003) commonly use the notation 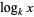 to denote the nested natural logarithm
to denote the nested natural logarithm 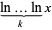 .
.
In the Wolfram Language, the logarithm to the base 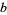 is implemented as Log[b, x], while Log[x] gives the natural logarithm, i.e., Log[E, x], where E is the Wolfram Language symbol for e.
is implemented as Log[b, x], while Log[x] gives the natural logarithm, i.e., Log[E, x], where E is the Wolfram Language symbol for e.
Whereas powers of trigonometric functions are denoted using notations like 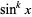 ,
, 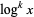 is less commonly used in favor of the notation
is less commonly used in favor of the notation 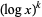 .
.
Logarithms are used in many areas of science and engineering in which quantities vary over a large range. For example, the decibel scale for the loudness of sound, the Richter scale of earthquake magnitudes, and the astronomical scale of stellar brightnesses are all logarithmic scales.
The derivative and indefinite integral of 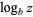 are given by
are given by
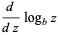 |
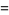 |
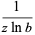 |
(3) |
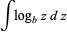 |
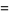 |
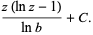 |
(4) |
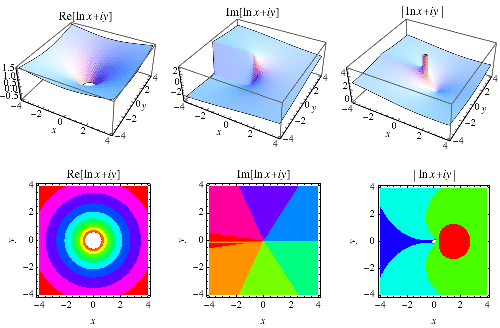 |
The logarithm can also be defined for complex arguments, as shown above. If the logarithm is taken as the forward function, the function taking the base to a given power is then called the antilogarithm.
For 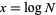 ,
, 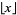 is called the characteristic, and
is called the characteristic, and 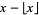 is called the mantissa.
is called the mantissa.
Division and multiplication identities for the logarithm can be derived from the identity
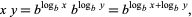 |
(5) |
including
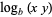 |
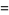 |
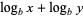 |
(6) |
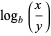 |
 |
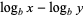 |
(7) |
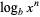 |
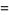 |
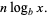 |
(8) |
There are a number of properties which can be used to change from one logarithm base to another, including
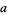 |
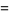 |
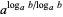 |
(9) |
 |
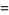 |
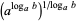 |
(10) |
 |
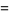 |
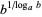 |
(11) |
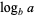 |
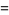 |
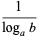 |
(12) |
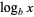 |
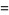 |
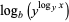 |
(13) |
 |
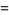 |
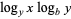 |
(14) |
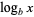 |
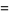 |
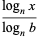 |
(15) |
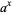 |
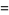 |
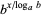 |
(16) |
 |
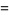 |
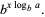 |
(17) |
An interesting property of logarithms follows from looking for a number  such that
such that
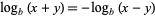 |
(18) |
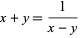 |
(19) |
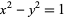 |
(20) |
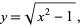 |
(21) |
so
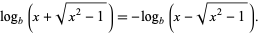 |
(22) |
Another related identity that holds for arbitrary 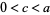 is given by
is given by
 |
(23) |
Numbers of the form 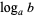 are irrational if
are irrational if 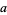 and
and 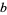 are integers, one of which has a prime factor which the other lacks. A. Baker made a major step forward in transcendental number theory by proving the transcendence of sums of numbers of the form
are integers, one of which has a prime factor which the other lacks. A. Baker made a major step forward in transcendental number theory by proving the transcendence of sums of numbers of the form 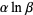 for
for 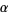 and
and 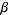 algebraic numbers.
algebraic numbers.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Logarithmic Function." §4.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 67-69, 1972.
Beyer, W. H. "Logarithms." CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 159-160 and 221, 1987.
Conway, J. H. and Guy, R. K. "Logarithms." The Book of Numbers. New York: Springer-Verlag, pp. 248-252, 1996.
Ivić, A. "On a Problem of Erdős Involving the Largest Prime Factor of 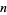 ." 5 Nov 2003. http://arxiv.org/abs/math.NT/0311056.
." 5 Nov 2003. http://arxiv.org/abs/math.NT/0311056.
Pappas, T. "Earthquakes and Logarithms." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 20-21, 1989.
Spanier, J. and Oldham, K. B. "The Logarithmic Function 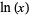 ." Ch. 25 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 225-232, 1987.
." Ch. 25 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 225-232, 1987.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|