المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | q-Dougall Sum |
 1266
 05:33 مساءً
date: 27-8-2019 |
Author : Bhatnagar, G 
Book or Source : Inverse Relations, Generalized Bibasic Series, and their U(n) Extensions. Ph.D. thesis. Ohio State University 
Page and Part : ...|
Read More
Date: 21-9-2019
1820
Date: 17-9-2019
1810
Date: 17-9-2018
1780
|
![_8phi_7[a,qa^(1/2),-qa^(1/2),b,c,d,e,q^(-N); a^(1/2),-a^(1/2),(aq)/b,(aq)/c,(aq)/d,(aq)/e,aq^(N+1);q,q]=(((aq)/(bd);q)_N((aq)/(cd);q)_N(aq;q)_N((aq)/(bc);q)_N)/(((aq)/(bd);q)_N((aq)/(bcd);q)_N((aq)/b;q)_N((aq)/c;q)_N),](http://mathworld.wolfram.com/images/equations/q-DougallSum/NumberedEquation1.gif) |
where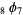 
is a q-hypergeometric function.
REFERENCES:
Bhatnagar, G. Inverse Relations, Generalized Bibasic Series, and their U(n) Extensions. Ph.D. thesis. Ohio State University, p. 36, 1995.
Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, p. 35, 1990.
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|
