


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-9-2018
Date: 26-8-2019
Date: 23-6-2019
|
Use the definition of the q-series
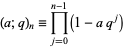 |
(1) |
and define
![[N; M]=((q^(N-M+1);q)_M)/((q;q)_m).](http://mathworld.wolfram.com/images/equations/BorweinConjectures/NumberedEquation2.gif) |
(2) |
Then P. Borwein has conjectured that (1) the polynomials 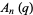 ,
, 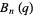 , and
, and 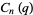 defined by
defined by
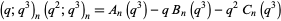 |
(3) |
have nonnegative coefficients, (2) the polynomials 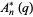 ,
, 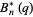 , and
, and 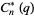 defined by
defined by
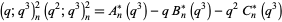 |
(4) |
have nonnegative coefficients, (3) the polynomials 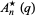 ,
, 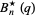 ,
, 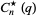 ,
, 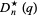 , and
, and 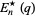 defined by
defined by
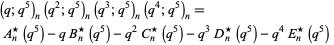 |
(5) |
have nonnegative coefficients, (4) the polynomials 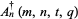 ,
, 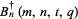 , and
, and 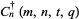 defined by
defined by
![(q;q^3)_m(q^2;q^3)_m(zq;q^3)_n(zq^2;q^3)_n
=sum_(t=0)^(2m)z^t[A^|(m,n,t,q^3)-qB^|(m,n,t,q^3)-q^2C^|(m,n,t,q^3)]](http://mathworld.wolfram.com/images/equations/BorweinConjectures/NumberedEquation6.gif) |
(6) |
have nonnegative coefficients, (5) for 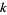 odd and
odd and 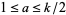 , consider the expansion
, consider the expansion
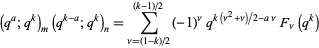 |
(7) |
with
![F_nu(q)=sum_(j=-infty)^infty(-1)^jq^(j(k^2j+2knu+k-2a)/2)[m+n; m+nu+kj],](http://mathworld.wolfram.com/images/equations/BorweinConjectures/NumberedEquation8.gif) |
(8) |
then if 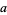 is relatively prime to
is relatively prime to 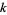 and
and 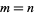 , the coefficients of
, the coefficients of 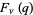 are nonnegative, and (6) given
are nonnegative, and (6) given 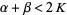 and
and 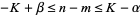 , consider
, consider
![G(alpha,beta,K;q)=sum_(q)(-1)^jq^(j[K(alpha+beta)j+K(alpha+beta)]/2)[m+n; m+Kj],](http://mathworld.wolfram.com/images/equations/BorweinConjectures/NumberedEquation9.gif) |
(9) |
the generating function for partitions inside an 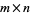 rectangle with hook difference conditions specified by
rectangle with hook difference conditions specified by 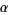 ,
, 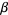 , and
, and 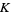 . Let
. Let 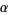 and
and 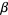 be positive rational numbers and
be positive rational numbers and 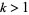 an integer such that
an integer such that 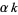 and
and 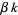 are integers. then if
are integers. then if 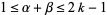 (with strict inequalities for
(with strict inequalities for 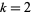 ) and
) and 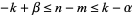 , then
, then 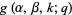 has nonnegative coefficients.
has nonnegative coefficients.
REFERENCES:
Andrews, G. E. et al. "Partitions with Prescribed Hook Differences." Europ. J. Combin. 8, 341-350, 1987.
Bressoud, D. M. "The Borwein Conjecture and Partitions with Prescribed Hook Differences." Electronic J. Combinatorics 3, No. 2, R4, 1-14, 1996. http://www.combinatorics.org/Volume_3/Abstracts/v3i2r4.html.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|