q-Binomial Theorem

The q-analog of the binomial theorem

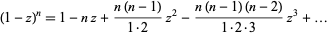(1)

is given by

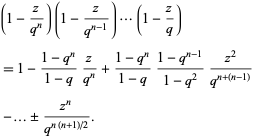(2)

Written as a q-series, the identity becomes

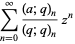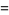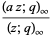			(3)
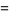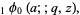			(4)

where 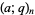 is a 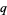-Pochhammer symbol and  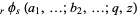is a 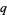-hypergeometric function (Heine 1847, p. 303; Andrews 1986). The Cauchy binomial theorem is a special case of this general theorem.

REFERENCES:

Andrews, G. E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., p. 10, 1986.

Bhatnagar, G. Inverse Relations, Generalized Bibasic Series, and their U(n) Extensions. Ph.D. thesis. Ohio State University, p. 24, 1995.

Gasper, G. "Elementary Derivations of Summation and Transformation Formulas for q-Series." In Fields Inst. Comm. 14 (Ed. M. E. H. Ismail et al. ), pp. 55-70, 1997.

Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, p. 7, 1990.

Heine, E. "Untersuchungen über die Reihe 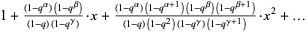." J. reine angew. Math. 34, 285-328, 1847.

Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, p. 26, 1998.