


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-6-2019
Date: 12-10-2018
Date: 18-6-2019
|
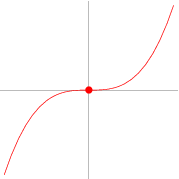
An inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. Inflection points may be stationary points, but are not local maxima or local minima. For example, for the curve 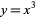 plotted above, the point
plotted above, the point 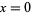 is an inflection point.
is an inflection point.
The first derivative test can sometimes distinguish inflection points from extrema for differentiable functions 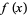 .
.
The second derivative test is also useful. A necessary condition for  to be an inflection point is
to be an inflection point is 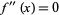 . A sufficient condition requires
. A sufficient condition requires  and
and 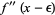 to have opposite signs in the neighborhood of
to have opposite signs in the neighborhood of  (Bronshtein and Semendyayev 2004, p. 231).
(Bronshtein and Semendyayev 2004, p. 231).
REFERENCES:
Bronshtein, I. N.; Semendyayev, K. A.; Musiol, G.; and Muehlig, H. Handbook of Mathematics, 4th ed. New York: Springer-Verlag, 2004.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
مؤسسة السجناء السياسيين: سجلنا 120 ألفًا من ضحايا السجون والاعتقالات في عهد النظام السابق
|
|
|