


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-9-2018
Date: 15-5-2019
Date: 17-3-2019
|
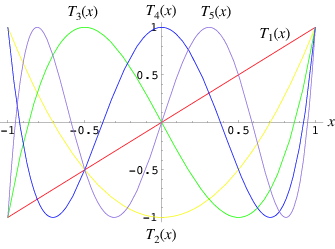
The Chebyshev polynomials of the first kind are a set of orthogonal polynomials defined as the solutions to the Chebyshev differential equation and denoted 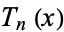 . They are used as an approximation to a least squares fit, and are a special case of the Gegenbauer polynomial with
. They are used as an approximation to a least squares fit, and are a special case of the Gegenbauer polynomial with  . They are also intimately connected with trigonometric multiple-angle formulas. The Chebyshev polynomials of the first kind are denoted
. They are also intimately connected with trigonometric multiple-angle formulas. The Chebyshev polynomials of the first kind are denoted  , and are implemented in the Wolfram Language as ChebyshevT[n, x]. They are normalized such that
, and are implemented in the Wolfram Language as ChebyshevT[n, x]. They are normalized such that 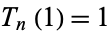 . The first few polynomials are illustrated above for
. The first few polynomials are illustrated above for ![x in [-1,1]](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/Inline5.gif) and
and 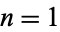 , 2, ..., 5.
, 2, ..., 5.
The Chebyshev polynomial of the first kind 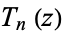 can be defined by the contour integral
can be defined by the contour integral
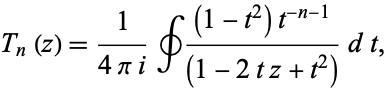 |
(1) |
where the contour encloses the origin and is traversed in a counterclockwise direction (Arfken 1985, p. 416).
The first few Chebyshev polynomials of the first kind are
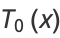 |
 |
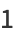 |
(2) |
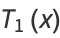 |
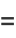 |
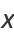 |
(3) |
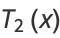 |
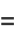 |
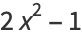 |
(4) |
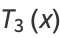 |
 |
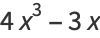 |
(5) |
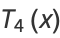 |
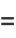 |
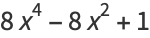 |
(6) |
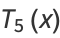 |
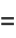 |
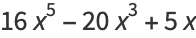 |
(7) |
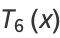 |
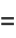 |
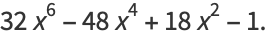 |
(8) |
When ordered from smallest to largest powers, the triangle of nonzero coefficients is 1; 1; 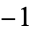 , 2;
, 2; 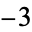 , 4; 1,
, 4; 1, 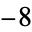 , 8; 5,
, 8; 5, 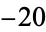 , 16, ... (OEIS A008310).
, 16, ... (OEIS A008310).

A beautiful plot can be obtained by plotting  radially, increasing the radius for each value of
radially, increasing the radius for each value of 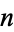 , and filling in the areas between the curves (Trott 1999, pp. 10 and 84).
, and filling in the areas between the curves (Trott 1999, pp. 10 and 84).
The Chebyshev polynomials of the first kind are defined through the identity
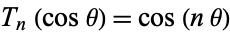 |
(9) |
The Chebyshev polynomials of the first kind can be obtained from the generating functions
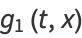 |
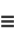 |
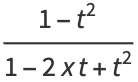 |
(10) |
 |
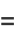 |
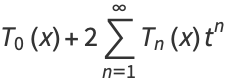 |
(11) |
and
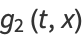 |
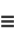 |
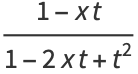 |
(12) |
 |
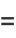 |
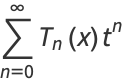 |
(13) |
for 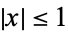 and
and 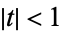 (Beeler et al. 1972, Item 15). (A closely related generating function is the basis for the definition of Chebyshev polynomial of the second kind.)
(Beeler et al. 1972, Item 15). (A closely related generating function is the basis for the definition of Chebyshev polynomial of the second kind.)
A direct representation is given by
![T_n(z)=1/2z^2[(sqrt(1-1/(z^2))+1)^n+(sqrt(1-1/(z^2)))^n].](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/NumberedEquation3.gif) |
(14) |
The polynomials can also be defined in terms of the sums
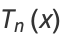 |
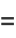 |
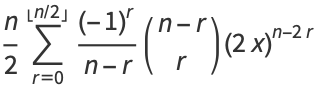 |
(15) |
 |
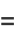 |
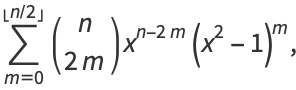 |
(16) |
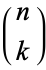 |
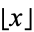 |
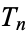 |
(17) |
where 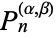 is a binomial coefficient and
is a binomial coefficient and 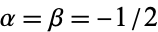 is the floor function, or the product
is the floor function, or the product
![T_n(x)=2^(n-1)product_(k=1)^n{x-cos[((2k-1)pi)/(2n)]}](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/NumberedEquation4.gif) |
(18) |
(Zwillinger 1995, p. 696).
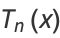 also satisfy the curious determinant equation
also satisfy the curious determinant equation
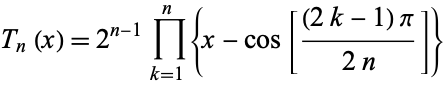 |
(19) |
(Nash 1986).
The Chebyshev polynomials of the first kind are a special case of the Jacobi polynomials 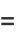 with
with 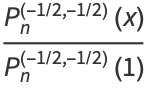 ,
,
 |
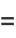 |
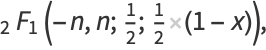 |
(20) |
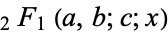 |
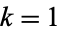 |
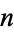 |
(21) |
where 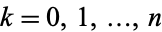 is a hypergeometric function (Koekoek and Swarttouw 1998).
is a hypergeometric function (Koekoek and Swarttouw 1998).
Zeros occur when
![x=cos[(pi(k-1/2))/n]](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/NumberedEquation6.gif) |
(22) |
for 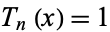 , 2, ...,
, 2, ..., 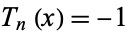 . Extrema occur for
. Extrema occur for
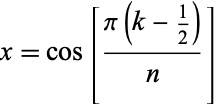 |
(23) |
where 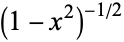 . At maximum,
. At maximum, 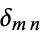 , and at minimum,
, and at minimum, 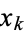 .
.
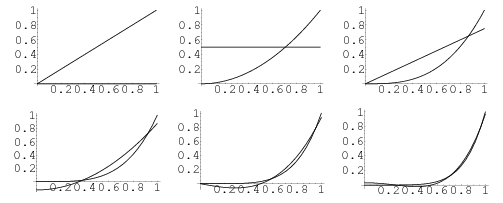
The Chebyshev polynomials are orthogonal polynomials with respect to the weighting function 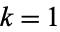
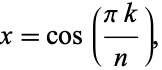 |
(24) |
where 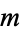 is the Kronecker delta. Chebyshev polynomials of the first kind satisfy the additional discrete identity
is the Kronecker delta. Chebyshev polynomials of the first kind satisfy the additional discrete identity
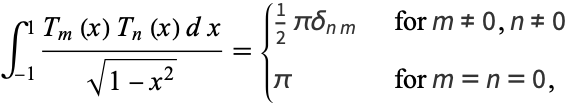 |
(25) |
where 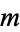 for
for 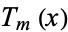 , ...,
, ..., 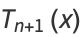 are the
are the 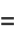 zeros of
zeros of 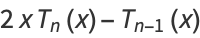 .
.
They also satisfy the recurrence relations
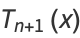 |
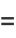 |
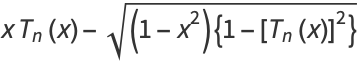 |
(26) |
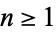 |
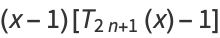 |
![xT_n(x)-sqrt((1-x^2){1-[T_n(x)]^2})](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/Inline87.gif) |
(27) |
for 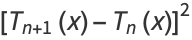 , as well as
, as well as
![(x-1)[T_(2n+1)(x)-1]](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/Inline89.gif) |
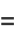 |
![[T_(n+1)(x)-T_n(x)]^2](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/Inline91.gif) |
(28) |
![2(x^2-1)[T_(2n)(x)-1]](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/Inline92.gif) |
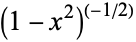 |
![[T_(n+1)(x)-T_(n-1)(x)]^2](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/Inline94.gif) |
(29) |
(Watkins and Zeitlin 1993; Rivlin 1990, p. 5).
They have a complex integral representation
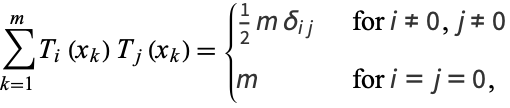 |
(30) |
and a Rodrigues representation
![T_n(x)=((-1)^nsqrt(pi)(1-x^2)^(1/2))/(2^n(n-1/2)!)(d^n)/(dx^n)[(1-x^2)^(n-1/2)].](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/NumberedEquation11.gif) |
(31) |
Using a fast Fibonacci transform with multiplication law
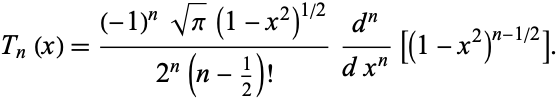 |
(32) |
gives
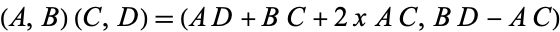 |
(33) |
Using Gram-Schmidt orthonormalization in the range (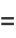 ,1) with weighting function
,1) with weighting function 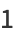 gives
gives
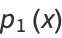 |
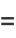 |
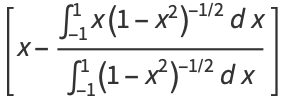 |
(34) |
 |
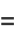 |
![[x-(int_(-1)^1x(1-x^2)^(-1/2)dx)/(int_(-1)^1(1-x^2)^(-1/2)dx)]](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/Inline102.gif) |
(35) |
 |
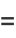 |
![x-([-(1-x^2)^(1/2)]_(-1)^1)/([sin^(-1)x]_(-1)^1)](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/Inline105.gif) |
(36) |
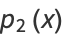 |
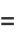 |
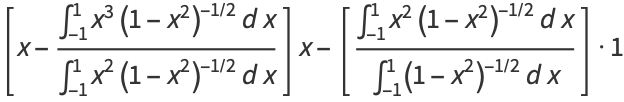 |
(37) |
 |
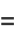 |
![[x-(int_(-1)^1x^3(1-x^2)^(-1/2)dx)/(int_(-1)^1x^2(1-x^2)^(-1/2)dx)]x-[(int_(-1)^1x^2(1-x^2)^(-1/2)dx)/(int_(-1)^1(1-x^2)^(-1/2)dx)]·1](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/Inline111.gif) |
(38) |
 |
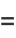 |
![[x-0]x-(pi/2)/pi](http://mathworld.wolfram.com/images/equations/ChebyshevPolynomialoftheFirstKind/Inline114.gif) |
(39) |
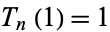 |
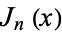 |
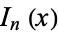 |
(40) |
etc. Normalizing such that 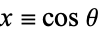 gives the Chebyshev polynomials of the first kind.
gives the Chebyshev polynomials of the first kind.
The Chebyshev polynomial of the first kind is related to the Bessel function of the first kind 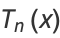 and modified Bessel function of the first kind
and modified Bessel function of the first kind 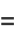 by the relations
by the relations
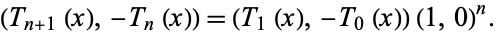 |
(41) |
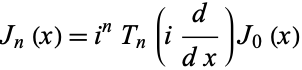 |
(42) |
Letting 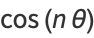 allows the Chebyshev polynomials of the first kind to be written as
allows the Chebyshev polynomials of the first kind to be written as
 |
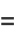 |
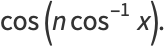 |
(43) |
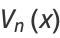 |
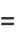 |
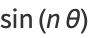 |
(44) |
The second linearly dependent solution to the transformed differential equation
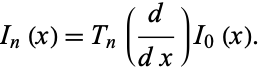 |
(45) |
is then given by
 |
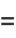 |
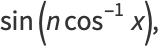 |
(46) |
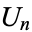 |
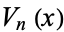 |
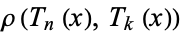 |
(47) |
which can also be written
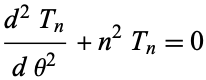 |
(48) |
where 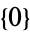 is a Chebyshev polynomial of the second kind. Note that
is a Chebyshev polynomial of the second kind. Note that 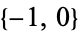 is therefore not a polynomial.
is therefore not a polynomial.
The triangle of resultants 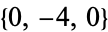 is given by
is given by 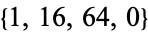 ,
, 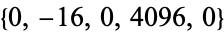 ,
, 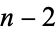 ,
, 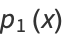 ,
, 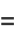 , ... (OEIS A054375).
, ... (OEIS A054375).
The polynomials
 |
(49) |
of degree 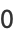 , the first few of which are
, the first few of which are
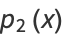 |
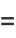 |
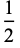 |
(50) |
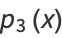 |
 |
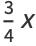 |
(51) |
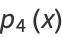 |
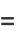 |
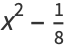 |
(52) |
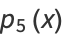 |
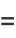 |
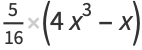 |
(53) |
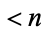 |
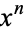 |
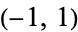 |
(54) |
are the polynomials of degree 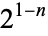 which stay closest to
which stay closest to 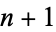 in the interval
in the interval 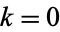 . The maximum deviation is
. The maximum deviation is 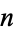 at the
at the 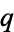 points where
points where
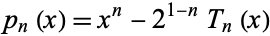 |
(55) |
for 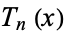 , 1, ...,
, 1, ..., 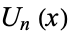 (Beeler et al. 1972).
(Beeler et al. 1972).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Orthogonal Polynomials." Ch. 22 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 771-802, 1972.
Arfken, G. "Chebyshev (Tschebyscheff) Polynomials" and "Chebyshev Polynomials--Numerical Applications." §13.3 and 13.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 731-748, 1985.
Beeler et al. Item 15 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 9, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/recurrence.html#item15.
Iyanaga, S. and Kawada, Y. (Eds.). "Čebyšev (Tschebyscheff) Polynomials." Appendix A, Table 20.II in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1478-1479, 1980.
Koekoek, R. and Swarttouw, R. F. "Chebyshev." §1.8.2 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 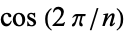 -Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 41-43, 1998.
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 41-43, 1998.
Koepf, W. "Efficient Computation of Chebyshev Polynomials." In Computer Algebra Systems: A Practical Guide (Ed. M. J. Wester). New York: Wiley, pp. 79-99, 1999.
Nash, P. L. "Chebyshev Polynomials and Quadratic Path Integrals." J. Math. Phys. 27, 2963, 1986.
Rivlin, T. J. Chebyshev Polynomials. New York: Wiley, 1990.
Shohat, J. Théorie générale des polynomes orthogonaux de Tchebichef. Paris: Gauthier-Villars, 1934.
Sloane, N. J. A. Sequences A008310 and A054375 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Chebyshev Polynomials 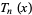 and
and 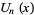 ." Ch. 22 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 193-207, 1987.
." Ch. 22 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 193-207, 1987.
Trott, M. Graphica 1: The World of Mathematica Graphics. The Imaginary Made Real: The Images of Michael Trott. Champaign, IL: Wolfram Media, pp. 10 and 84, 1999.
Vasilyev, N. and Zelevinsky, A. "A Chebyshev Polyplayground: Recurrence Relations Applied to a Famous Set of Formulas." Quantum 10, 20-26, Sept./Oct. 1999.
Watkins, W. and Zeitlin, J. "The Minimal Polynomial of 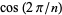 ." Amer. Math. Monthly 100, 471-474, 1993.
." Amer. Math. Monthly 100, 471-474, 1993.
Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, 1995.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|