


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-4-2019
Date: 25-3-2019
Date: 19-5-2019
|
A 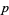 -variate multivariate normal distribution (also called a multinormal distribution) is a generalization of the bivariate normal distribution. The
-variate multivariate normal distribution (also called a multinormal distribution) is a generalization of the bivariate normal distribution. The 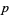 -multivariate distribution with mean vector
-multivariate distribution with mean vector 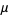 and covariance matrix
and covariance matrix 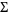 is denoted
is denoted 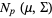 . The multivariate normal distribution is implemented as MultinormalDistribution[
. The multivariate normal distribution is implemented as MultinormalDistribution[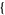 mu1, mu2, ...
mu1, mu2, ...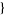 ,
, 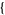
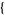 sigma11, sigma12, ...
sigma11, sigma12, ...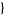 ,
, 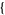 sigma12, sigma22, ...,
sigma12, sigma22, ..., 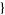 ...
...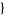 ,
, 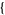 x1, x2, ...
x1, x2, ...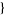 ] in the Wolfram Language package MultivariateStatistics` (where the matrix
] in the Wolfram Language package MultivariateStatistics` (where the matrix 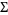 must be symmetric since
must be symmetric since 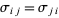 ).
).
In the case of nonzero correlations, there is in general no closed-form solution for the distribution function of a multivariate normal distribution. As a result, such computations must be done numerically.
REFERENCES:
Rose, C. and Smith, M. D. "The Multivariate Normal Distribution." Mathematica J. 6, 32-37, 1996.
Rose, C. and Smith, M. D. "Random[Title]: Manipulating Probability Density Functions." Ch. 16 in Computational Economics and Finance: Modeling and Analysis with Mathematica (Ed. H. Varian). New York: Springer-Verlag, 1996.
Rose, C. and Smith, M. D. "The Multivariate Normal Distribution." §6.4 in Mathematical Statistics with Mathematica. New York: Springer-Verlag, pp. 216-235, 2002.
Schervish, M. J. "Multivariate Normal Probabilities with Error Bounds." Appl. Stat.: J. Roy. Stat. Soc., Ser. C 33, 81-94, 1984.
Schervish, M. J. "Corrections to Multivariate Normal Probabilities with Error Bounds." Appl. Stat.: J. Roy. Stat. Soc., Ser. C 34, 103-104, 1984.
Tong, L. The Multivariate Normal Distribution. New York: Springer-Verlag, 1990.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|