


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-6-2019
Date: 18-7-2019
Date: 12-10-2018
|
For all integers 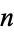 and nonnegative integers
and nonnegative integers 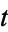 , the harmonic logarithms
, the harmonic logarithms 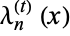 of order
of order 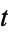 and degree
and degree 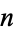 are defined as the unique functions satisfying
are defined as the unique functions satisfying
1. 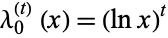 ,
,
2. 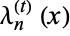 has no constant term except
has no constant term except 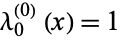 ,
,
3. ![d/(dx)lambda_n^((t))(x)=|_n]lambda_(n-1)^((t))(x)](http://mathworld.wolfram.com/images/equations/HarmonicLogarithm/Inline9.gif) ,
,
where the "Roman symbol" ![|_n]](http://mathworld.wolfram.com/images/equations/HarmonicLogarithm/Inline10.gif) is defined by
is defined by
![|_n]={n for n!=0; 1 for n=0](http://mathworld.wolfram.com/images/equations/HarmonicLogarithm/NumberedEquation1.gif) |
(1) |
(Roman 1992). This gives the special cases
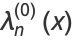 |
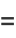 |
 |
(2) |
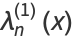 |
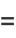 |
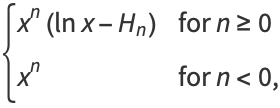 |
(3) |
where 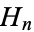 is a harmonic number. The harmonic logarithm has the integral
is a harmonic number. The harmonic logarithm has the integral
![intlambda_n^((1))(x)dx=1/(|_n+1])lambda_(n+1)^((1))(x).](http://mathworld.wolfram.com/images/equations/HarmonicLogarithm/NumberedEquation2.gif) |
(4) |
The harmonic logarithm can be written
![lambda_n^((t))(x)=|_n]!D^~^(-n)(lnx)^t,](http://mathworld.wolfram.com/images/equations/HarmonicLogarithm/NumberedEquation3.gif) |
(5) |
where 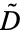 is the differential operator, (so
is the differential operator, (so 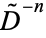 is the
is the 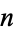 th integral). Rearranging gives
th integral). Rearranging gives
![D^~^klambda_n^((t))(x)=|_(|_n]!)/(|_n-k])]!lambda_(n-k)^((t))(x).](http://mathworld.wolfram.com/images/equations/HarmonicLogarithm/NumberedEquation4.gif) |
(6) |
This formulation gives an analog of the binomial theorem called the logarithmic binomial theorem. Another expression for the harmonic logarithm is
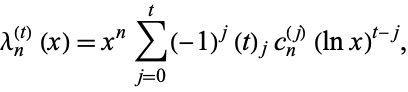 |
(7) |
where 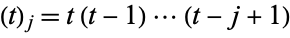 is a Pochhammer symbol and
is a Pochhammer symbol and 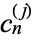 is a two-index harmonic number (Roman 1992).
is a two-index harmonic number (Roman 1992).
REFERENCES:
Loeb, D. and Rota, G.-C. "Formal Power Series of Logarithmic Type." Advances Math. 75, 1-118, 1989.
Roman, S. "The Logarithmic Binomial Formula." Amer. Math. Monthly 99, 641-648, 1992.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
مكتب المرجع الديني الأعلى يعزّي باستشهاد عددٍ من المؤمنين في باكستان
|
|
|