


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-9-2019
Date: 22-9-2019
Date: 21-8-2018
|
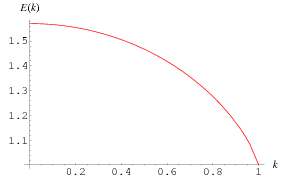
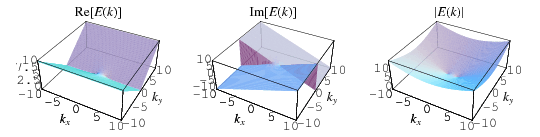
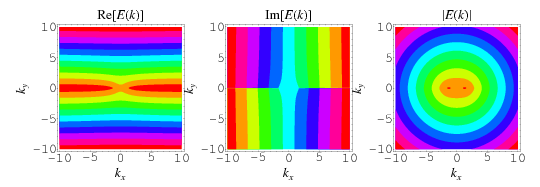
The complete elliptic integral of the second kind, illustrated above as a function of 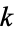 , is defined by
, is defined by
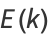 |
 |
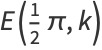 |
(1) |
 |
 |
![pi/2{1-sum_(n=1)^(infty)[((2n-1)!!)/((2n)!!)]^2(k^(2n))/(2n-1)}](http://mathworld.wolfram.com/images/equations/CompleteEllipticIntegraloftheSecondKind/Inline7.gif) |
(2) |
 |
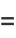 |
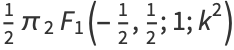 |
(3) |
 |
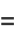 |
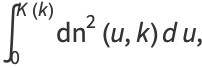 |
(4) |
where 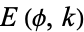 is an incomplete elliptic integral of the second kind,
is an incomplete elliptic integral of the second kind, 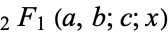 is the hypergeometric function, and
is the hypergeometric function, and 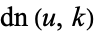 is a Jacobi elliptic function.
is a Jacobi elliptic function.
It is implemented in the Wolfram Language as EllipticE[m], where 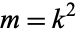 is the parameter.
is the parameter.
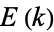 can be computed in closed form in terms of
can be computed in closed form in terms of 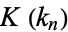 and the elliptic alpha function
and the elliptic alpha function 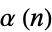 for special values of
for special values of 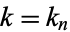 , where
, where 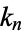 is a called an elliptic integral singular value. Other special values include
is a called an elliptic integral singular value. Other special values include
 |
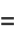 |
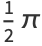 |
(5) |
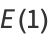 |
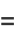 |
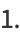 |
(6) |
The complete elliptic integral of the second kind satisfies the Legendre relation
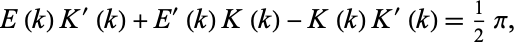 |
(7) |
where 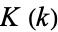 and
and 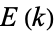 are complete elliptic integrals of the first and second kinds, respectively, and
are complete elliptic integrals of the first and second kinds, respectively, and 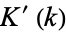 and
and 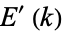 are the complementary integrals. The derivative is
are the complementary integrals. The derivative is
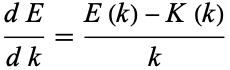 |
(8) |
(Whittaker and Watson 1990, p. 521).
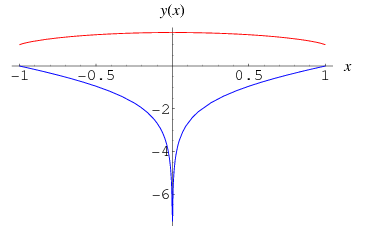
The solution to the differential equation
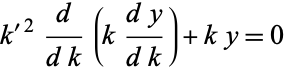 |
(9) |
(Zwillinger 1997, p. 122; Gradshteyn and Ryzhik 2000, p. 907) is given by
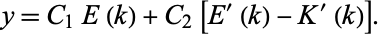 |
(10) |
If 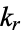 is a singular value (i.e.,
is a singular value (i.e.,
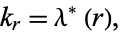 |
(11) |
where 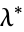 is the elliptic lambda function), and
is the elliptic lambda function), and 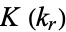 and the elliptic alpha function
and the elliptic alpha function 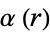 are also known, then
are also known, then
![E(k)=(K(k))/(sqrt(r))[pi/(3[K(k)]^2)-alpha(r)]+K(k).](http://mathworld.wolfram.com/images/equations/CompleteEllipticIntegraloftheSecondKind/NumberedEquation6.gif) |
(12) |
REFERENCES:
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 122, 1997.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|