


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-2-2019
Date: 19-1-2019
Date: 17-1-2019
|
If 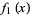 , ...,
, ..., 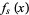 are irreducible polynomials with integer coefficients such that no integer
are irreducible polynomials with integer coefficients such that no integer 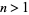 divides
divides 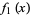 , ...,
, ..., 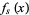 for all integers
for all integers  , then there should exist infinitely many
, then there should exist infinitely many  such that
such that 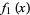 , ...,
, ..., 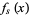 are simultaneously prime.
are simultaneously prime.
If Schinzel's hypothesis is true, then it follows that all positive integers 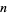 can be represented in the form
can be represented in the form 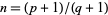 with
with 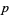 and
and 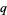 prime. In addition, it would follow that there are an infinite number of numbers
prime. In addition, it would follow that there are an infinite number of numbers 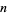 such that
such that 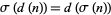 , where
, where 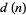 is the number of divisors of
is the number of divisors of 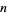 and
and 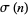 is the sum of divisors, since the conjecture implies that there are infinitely many primes
is the sum of divisors, since the conjecture implies that there are infinitely many primes 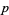 for which
for which 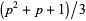 is prime, for such
is prime, for such 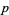 ,
, 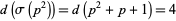 and
and 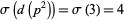 , so
, so 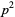 is in the sequence (D. Hickerson, pers. comm., Jan. 24, 2006).
is in the sequence (D. Hickerson, pers. comm., Jan. 24, 2006).
Conroy (2001) verified the conjecture to 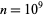 .
.
REFERENCES:
Conroy, M. M. "A Sequence Related to a Conjecture of Schinzel." J. Integer Sequences 4, No. 01.1.7, 2001. http://www.cs.uwaterloo.ca/journals/JIS/VOL4/CONROY/conroy.html.
Dickson, L. E. "A New Extension of Dirichlet's Theorem on Prime Numbers." Messenger Math. 33, 155-161, 1904.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.
Schinzel, A. and Sierpiński, W. "Sur certaines hypothèses concernant les nombres premiers. Remarque." Acta Arithm. 4, 185-208, 1958.
Schinzel, A. and Sierpiński, W. Erratum to "Sur certains hypothèses concernant les nombres premiers." Acta Arith. 5, 259, 1959.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|