dditive Polynomial

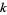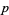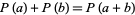Let  be a field of finite characteristic . Then a polynomial  is said to be additive iff  for 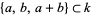. For example,  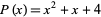is additive for 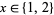, since

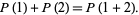A more interesting class of additive polynomials known as absolutely additive polynomials are defined on an algebraic closure 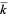 of 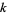. For example, for any such 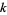,  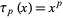is an absolutely additive polynomial, since 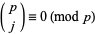, for 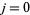, ..., 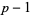. The polynomial  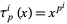is also absolutely additive.

Let the ring of polynomials spanned by linear combinations of 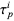 be denoted . If 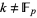, then  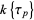is not commutative.

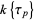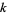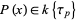Not all additive polynomials are in . In particular, if  is an infinite field, then a polynomial  is additive iff . For 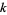 be a finite field of characteristic 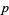, the set of absolutely additive polynomials over  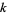equals 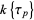, so the qualification "absolutely" can be dropped and the term "additive" alone can be used to refer to an element of .

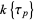If 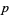 is a fixed power  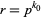and 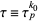, then  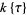is a ring of polynomials in . Moreover, if 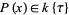, then  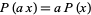for all 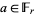. In this case,  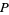is said to be a 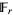-linear polynomial.

The fundamental theorem of additive polynomials states that if  is a separable polynomial and 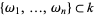 is the set of its roots, then  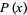is additive iff if  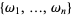is a subgroup.

It therefore follows as a corollary that such a polynomial 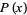 is 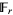-linear iff its roots form a 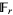-vector subspace of .

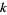REFERENCES:

Goss, D. Basic Structures of Function Field Arithmetic. Berlin: Springer-Verlag, pp. 1-33, 1996.