


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-11-2018
Date: 22-11-2018
Date: 1-11-2018
|
 |
The absolute value of a real number  is denoted
is denoted 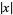 and defined as the "unsigned" portion of
and defined as the "unsigned" portion of  ,
,
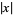 |
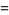 |
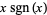 |
(1) |
 |
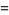 |
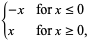 |
(2) |
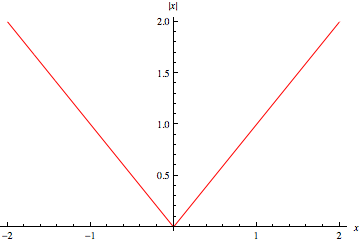
where 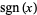 is the sign function. The absolute value is therefore always greater than or equal to 0. The absolute value of
is the sign function. The absolute value is therefore always greater than or equal to 0. The absolute value of  for real
for real  is plotted above.
is plotted above.
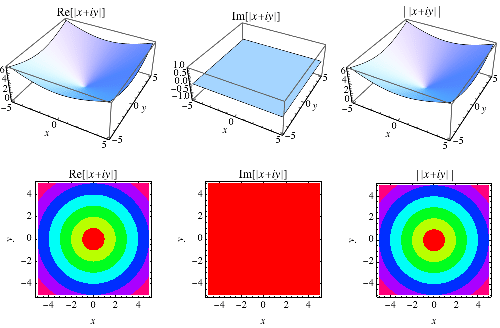 |
The absolute value of a complex number 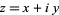 , also called the complex modulus, is defined as
, also called the complex modulus, is defined as
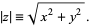 |
(3) |
This form is implemented in the Wolfram Language as Abs[z] and is illustrated above for complex 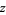 .
.
Note that the derivative (read: complex derivative) 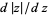 does not exist because at every point in the complex plane, the value of the derivative of
does not exist because at every point in the complex plane, the value of the derivative of 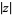 depends on the direction in which the derivative is taken (so the Cauchy-Riemann equations cannot and do not hold). However, the real derivative (i.e., restricting the derivative to directions along the real axis) can be defined for points other than
depends on the direction in which the derivative is taken (so the Cauchy-Riemann equations cannot and do not hold). However, the real derivative (i.e., restricting the derivative to directions along the real axis) can be defined for points other than 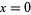 as
as
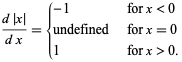 |
(4) |
As a result of the fact that computer algebra languages such as the Wolfram Language generically deal with complex variables (i.e., the definition of derivative always means complex derivative), 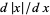 correctly returns unevaluated by such software.
correctly returns unevaluated by such software.
Note that the notation 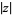 is commonly used to denote the complex modulus, p-adic norm, or general valuation. In this work, the norm of a vector
is commonly used to denote the complex modulus, p-adic norm, or general valuation. In this work, the norm of a vector  is also denoted
is also denoted 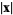 , although the notation
, although the notation 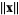 is also in common use.
is also in common use.
The notations for the floor function 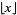 , nearest integer function
, nearest integer function ![[x]](http://mathworld.wolfram.com/images/equations/AbsoluteValue/Inline24.gif) , and ceiling function
, and ceiling function ![[x]](http://mathworld.wolfram.com/images/equations/AbsoluteValue/Inline25.gif) are similar to that used for the absolute value.
are similar to that used for the absolute value.
The unit square integral of the absolute value of the difference of two variables taken to the power 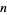 is given by
is given by
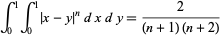 |
(5) |
for ![R[n]>-1](http://mathworld.wolfram.com/images/equations/AbsoluteValue/Inline27.gif) , which has values for
, which has values for 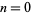 , 1, ... of 1, 1/3, 1/6, 1/10, 1/15, 1/21, ..., i.e., one over the triangular numbers (OEIS A000217), for
, 1, ... of 1, 1/3, 1/6, 1/10, 1/15, 1/21, ..., i.e., one over the triangular numbers (OEIS A000217), for 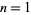 , 2, .... This sort of integral arises in the study of the Casimir effect (Milton and Ng 1998, eqn. 3.15; Milton 1999, p. 32, eqn. 3.33).
, 2, .... This sort of integral arises in the study of the Casimir effect (Milton and Ng 1998, eqn. 3.15; Milton 1999, p. 32, eqn. 3.33).
Similarly, for ![R[n]>-2](http://mathworld.wolfram.com/images/equations/AbsoluteValue/Inline30.gif) ,
,
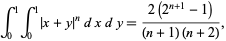 |
(6) |
giving the first few values for 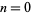 , 1, ... of 1, 1, 7/6, 3/2, 31, 15, 3, ... (OEIS A116419 and A116420).
, 1, ... of 1, 1, 7/6, 3/2, 31, 15, 3, ... (OEIS A116419 and A116420).
REFERENCES:
Milton, K. A. "The Casimir Effect: Physical Manifestations of Zero-Point Energy." 4 Jan 1999. http://arxiv.org/abs/hep-th/9901011.
Milton, K. A. and Ng, J. "Observability of the Bulk Casimir Effect: Can the Dynamical Casimir Effect be Relevant to Sonoluminescence?" Phys. Rev. E 57, 5504-5510, 1998.
Sloane, N. J. A. Sequences A000217/M2535, A116419, and A116420 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|