


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-8-2019
Date: 12-8-2018
Date:
|
The supremum is the least upper bound of a set 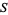 , defined as a quantity
, defined as a quantity 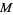 such that no member of the set exceeds
such that no member of the set exceeds 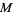 , but if
, but if 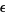 is any positive quantity, however small, there is a member that exceeds
is any positive quantity, however small, there is a member that exceeds 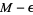 (Jeffreys and Jeffreys 1988). When it exists (which is not required by this definition, e.g.,
(Jeffreys and Jeffreys 1988). When it exists (which is not required by this definition, e.g., 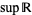 does not exist), it is denoted
does not exist), it is denoted 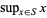 (or sometimes simply
(or sometimes simply 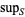 for short). The supremum is implemented in the Wolfram Language as MaxValue[f, constr, vars].
for short). The supremum is implemented in the Wolfram Language as MaxValue[f, constr, vars].
More formally, the supremum 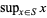 for
for 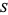 a (nonempty) subset of the affinely extended real numbers
a (nonempty) subset of the affinely extended real numbers 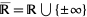 is the smallest value
is the smallest value 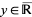 such that for all
such that for all 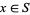 we have
we have 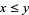 . Using this definition,
. Using this definition, 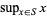 always exists and, in particular,
always exists and, in particular, 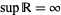 .
.
Whenever a supremum exists, its value is unique. On the real line, the supremum of a set is the same as the supremum of its set closure.
Consider the real numbers with their usual order. Then for any set 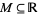 , the supremum
, the supremum 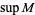 exists (in
exists (in 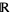 ) if and only if
) if and only if 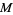 is bounded from above and nonempty.
is bounded from above and nonempty.
REFERENCES:
Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, p. 2, 1991.
Jeffreys, H. and Jeffreys, B. S. "Upper and Lower Bounds." §1.044 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, p. 13, 1988.
Knopp, K. Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, p. 6, 1996.
Royden, H. L. Real Analysis, 3rd ed. New York: Macmillan, p. 31, 1988.
Rudin, W. Real and Complex Analysis, 3rd ed. New York: McGraw-Hill, p. 7, 1987.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|