


 علم الكيمياء
علم الكيمياء 
 الكيمياء التحليلية
الكيمياء التحليلية 
 الكيمياء الحياتية
الكيمياء الحياتية 
 الكيمياء العضوية
الكيمياء العضوية 
 الكيمياء الفيزيائية
الكيمياء الفيزيائية
 الكيمياء اللاعضوية
الكيمياء اللاعضوية 
 مواضيع اخرى في الكيمياء
مواضيع اخرى في الكيمياء
 الكيمياء الصناعية
الكيمياء الصناعية |
Read More
Date: 13-8-2018
Date: 15-9-2019
Date: 2-1-2020
|
The following features lead to the nmr phenomenon:
1. A spinning charge generates a magnetic field, as shown by the animation on the right.
The resulting spin-magnet has a magnetic moment (μ) proportional to the spin.

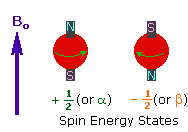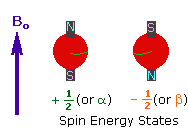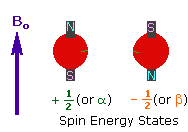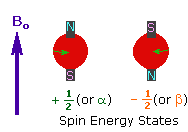
2. In the presence of an external magnetic field (B0), two spin states exist, +1/2 and -1/2.
The magnetic moment of the lower energy +1/2 state is aligned with the external field, but that of the higher energy -1/2 spin state is opposed to the external field. Note that the arrow representing the external field points North.
3. The difference in energy between the two spin states is dependent on the external magnetic field strength, and is always very small. The following diagram illustrates that the two spin states have the same energy when the external field is zero, but diverge as the field increases. At a field equal to Bx a formula for the energy difference is given (remember I = 1/2 and μ is the magnetic moment of the nucleus in the field).
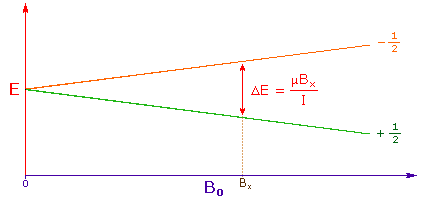
Strong magnetic fields are necessary for nmr spectroscopy. The international unit for magnetic flux is the tesla (T). The earth's magnetic field is not constant, but is approximately 10-4 T at ground level. Modern nmr spectrometers use powerful magnets having fields of 1 to 20 T. Even with these high fields, the energy difference between the two spin states is less than 0.1 cal/mole. To put this in perspective, recall that infrared transitions involve 1 to 10 kcal/mole and electronic transitions are nearly 100 time greater.
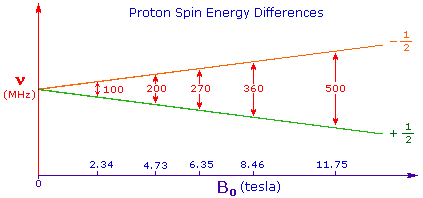
For nmr purposes, this small energy difference (ΔE) is usually given as a frequency in units of MHz (106 Hz), ranging from 20 to 900 Mz, depending on the magnetic field strength and the specific nucleus being studied. Irradiation of a sample with radio frequency (rf) energy corresponding exactly to the spin state separation of a specific set of nuclei will cause excitation of those nuclei in the +1/2 state to the higher -1/2 spin state. Note that this electromagnetic radiation falls in the radio and television broadcast spectrum. Nmr spectroscopy is therefore the energetically mildest probe used to examine the structure of molecules.
The nucleus of a hydrogen atom (the proton) has a magnetic moment μ = 2.7927, and has been studied more than any other nucleus. The previous diagram may be changed to display energy differences for the proton spin states (as frequencies) by mouse clicking anywhere within it.
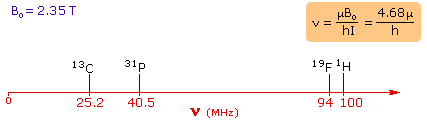
4. For spin 1/2 nuclei the energy difference between the two spin states at a given magnetic field strength will be proportional to their magnetic moments. For the four common nuclei noted above, the magnetic moments are: 1H μ = 2.7927, 19F μ = 2.6273, 31P μ = 1.1305 & 13C μ = 0.7022. These moments are in nuclear magnetons, which are 5.05078•10-27 JT-1. The following diagram gives the approximate frequencies that correspond to the spin state energy separations for each of these nuclei in an external magnetic field of 2.35 T. The formula in the colored box shows the direct correlation of frequency (energy difference) with magnetic moment (h = Planck's constant = 6.626069•10-34 Js).


|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|