Helmholtz Differential Equation

An elliptic partial differential equation given by

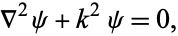(1)

where 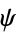 is a scalar function and  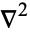is the scalar Laplacian, or

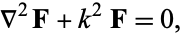(2)

where 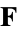 is a vector function and  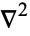is the vector Laplacian (Moon and Spencer 1988, pp. 136-143).

When 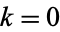, the Helmholtz differential equation reduces to Laplace's equation. When  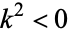(i.e., for imaginary 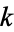), the equation becomes the space part of the diffusion equation.

The Helmholtz differential equation can be solved by separation of variables in only 11 coordinate systems, 10 of which (with the exception of confocal paraboloidal coordinates) are particular cases of the confocal ellipsoidal system: Cartesian, confocal ellipsoidal, confocal paraboloidal, conical, cylindrical, elliptic cylindrical, oblate spheroidal, paraboloidal, parabolic cylindrical, prolate spheroidal, and spherical coordinates (Eisenhart 1934ab). Laplace's equation (the Helmholtz differential equation with 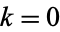) is separable in the two additional bispherical coordinates and toroidal coordinates.

If Helmholtz's equation is separable in a three-dimensional coordinate system, then Morse and Feshbach (1953, pp. 509-510) show that

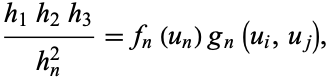(3)

where 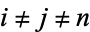. The Laplacian is therefore of the form

(4)

which simplifies to

(5)

Such a coordinate system obeys the Robertson condition, which means that the Stäckel determinant is of the form

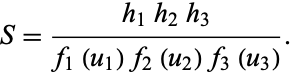(6)

REFERENCES:

Eisenhart, L. P. "Separable Systems in Euclidean 3-Space." Physical Review 45, 427-428, 1934a.

Eisenhart, L. P. "Separable Systems of Stäckel." Ann. Math. 35, 284-305, 1934b.

Eisenhart, L. P. "Potentials for Which Schroedinger Equations Are Separable." Phys. Rev. 74, 87-89, 1948.

Kriezis, E. E.; Tsiboukis, T. D.; Panas, S. M.; and Tegopoulos, J. A. "Eddy Currents:theory and Applications,." Proc. IEEE 80, 1559-1589, 1992.

Moon, P. and Spencer, D. E. "Eleven Coordinate Systems" and "The Vector Helmholtz Equation." §1 and 5 in Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, pp. 1-48 and 136-143, 1988.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 125-126, 271, and 509-510, 1953.

Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, p. 417, 1995.

Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 129, 1997.