المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر
أضيف حديثاً
تنفيذ وتقييم خطة إعادة الهيكلة (إعداد خطة إعادة الهيكلة1)
2024-11-05
مـعاييـر تحـسيـن الإنـتاجـيـة
2024-11-05
نـسـب الإنـتاجـيـة والغـرض مـنها
2024-11-05
المـقيـاس الكـلـي للإنتاجـيـة
2024-11-05
الإدارة بـمؤشـرات الإنـتاجـيـة (مـبادئ الإنـتـاجـيـة)
2024-11-05
زكاة الفطرة
2024-11-05

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
شروط الاعتراض في التشريعات المعتمدة لنظام الضريبة على القيمة المضافة
12-4-2022
الوظائف المستخدمة في تحديد الاقليم الوظيفي للمدينة
23/10/2022
ما يستحب ويكره عند المحتضر قبل خروج الروح.
20-1-2016
الدعاء لنصر الإسلام
26-9-2021
مفهوم الحرارة عند أنكسمندار (القرن 6 ق.م.)
2023-04-16
Energy Density in an Electric Field
20-12-2020

Helmholtz Differential Equation--Parabolic Coordinates  
  
1129   02:54 مساءً   date: 18-7-2018
Author : Moon, P. and Spencer, D. E
Book or Source : Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag
Page and Part : ...


Read More
Caudrey-Dodd-Gibbon-Sawada-Kotera Equation
Date: 13-7-2018 984
Helmholtz Differential Equation--Polar Coordinates
Date: 18-7-2018 1109
Landau-Lifshitz Equation
Date: 21-7-2018 1009

Helmholtz Differential Equation--Parabolic Coordinates

The scale factors are 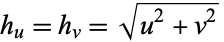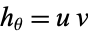h_u=h_v=sqrt(u^2+v^2), h_theta=uv and the separation functions are 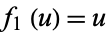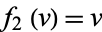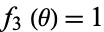f_1(u)=u, f_2(v)=v, f_3(theta)=1, given a Stäckel determinant of 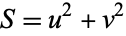S=u^2+v^2. The Laplacian is

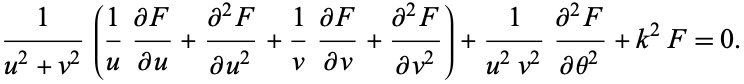1/(u^2+v^2)(1/u(partialF)/(partialu)+(partial^2F)/(partialu^2)+1/v(partialF)/(partialv)+(partial^2F)/(partialv^2))+1/(u^2v^2)(partial^2F)/(partialtheta^2)+k^2F=0.
(1)

Attempt separation of variables by writing

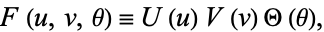F(u,v,theta)=U(u)V(v)Theta(theta),
(2)

then the Helmholtz differential equation becomes

1/(u^2+v^2)[VTheta(1/u(dU)/(du)+(d^2U)/(du^2))+UTheta(1/v(dV)/(dv)+(d^2V)/(dv^2))] +(UV)/(u^2v^2)(d^2Theta)/(dtheta^2)+k^2UVTheta=0.
(3)

Now multiply through by 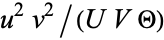u^2v^2/(UVTheta),

(u^2v^2)/(u^2+v^2)[1/U(1/u(dU)/(du)+(d^2U)/(du^2))+1/V(1/v(dV)/(dv)+(d^2V)/(dv^2))] +1/Theta(d^2Theta)/(dtheta^2)+k^2u^2v^2=0.
(4)

Separating the 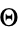Theta part gives

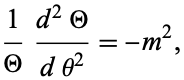1/Theta(d^2Theta)/(dtheta^2)=-m^2,
(5)

which has solution

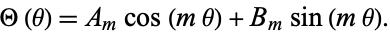Theta(theta)=A_mcos(mtheta)+B_msin(mtheta).
(6)

Plugging (5) back into (4) and multiplying by 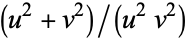(u^2+v^2)/(u^2v^2) gives

[1/U(1/u(dU)/(du)+(d^2U)/(du^2))+1/V(1/v(dV)/(dv)+(d^2V)/(dv^2))] -m^2(u^2+v^2)/(u^2v^2)+k^2(u^2+v^2).
(7)

Rewriting,

[1/U(1/u(dU)/(du)+(d^2U)/(du^2))+1/V(1/v(dV)/(dv)+(d^2V)/(dv^2))] -m^2(1/(v^2)+1/(u^2))+k^2(u^2+v^2).
(8)

This can be rearranged into two terms, each containing only 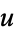u or v,

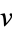[1/U(1/u(dU)/(du)+(d^2U)/(du^2))+k^2u^2-(m^2)/(u^2)] +[1/V(1/v(dV)/(dv)+(d^2V)/(dv^2))+k^2v^2-(m^2)/(v^2)]
(9)

and so can be separated by letting the first part equal 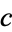c and the second equal 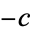-c, giving

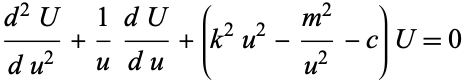(d^2U)/(du^2)+1/u(dU)/(du)+(k^2u^2-(m^2)/(u^2)-c)U=0
(10)

(d^2V)/(dv^2)+1/v(dV)/(dv)+(k^2v^2-(m^2)/(v^2)+c)V=0.

 

REFERENCES:

Arfken, G. "Parabolic Coordinates (xi,eta,phi)." §2.12 in Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 109-111, 1970.

Moon, P. and Spencer, D. E. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, p. 36, 1988.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York McGraw-Hill, pp. 514-515 and 660, 1953.



الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
التاريخ / 2024-11-04

الأخبار العلمية
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
التاريخ / 2024-11-04

الساحة الاسلامية
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
التاريخ / 2024-11-05