Elliptic Partial Differential Equation

A second-order partial differential equation, i.e., one of the form

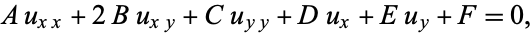(1)

is called elliptic if the matrix

(2)

is positive definite. Elliptic partial differential equations have applications in almost all areas of mathematics, from harmonic analysis to geometry to Lie theory, as well as numerous applications in physics. As with a general PDE, elliptic PDE may have non-constant coefficients and be non-linear. Despite this variety, the elliptic equations have a well-developed theory.

The basic example of an elliptic partial differential equation is Laplace's equation

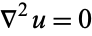(3)

in 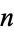-dimensional Euclidean space, where the Laplacian  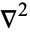is defined by

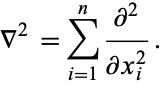(4)

Other examples of elliptic equations include the nonhomogeneous Poisson's equation

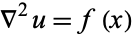(5)

and the non-linear minimal surface equation.

For an elliptic partial differential equation, boundary conditions are used to give the constraint 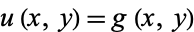 on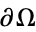, where

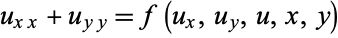(6)

holds in .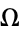

One property of constant coefficient elliptic equations is that their solutions can be studied using the Fourier transform. Consider Poisson's equation with periodic 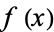. The Fourier series expansion is then given by

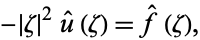(7)

where 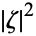 is called the "principal symbol," and so we can solve for 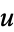. Except for 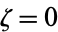, the multiplier is nonzero.

In general, a PDE may have non-constant coefficients or even be non-linear. A linear PDE is elliptic if its principal symbol, as in the theory of pseudodifferential operators, is nonzero away from the origin. For instance, (◇) has as its principal symbol 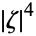, which is nonzero for 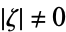, and is an elliptic PDE.

A nonlinear PDE is elliptic at a solution 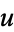 if its linearization is elliptic at 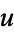. One simply calls a non-linear equation elliptic if it is elliptic at any solution, such as in the case of harmonic maps between Riemannian manifolds.